N88-BASICでレイトレーシング (8回目)

2021/6/8(火)

N88-BASICでレイトレーシング (8回目)

 

(by ULproject for N88-BASIC, NL-BASIC)

(NL-BASICはAlt+6で高速化します)

 

 

透過を追加します

透過は屈折光と反射光に分けて追跡します

 

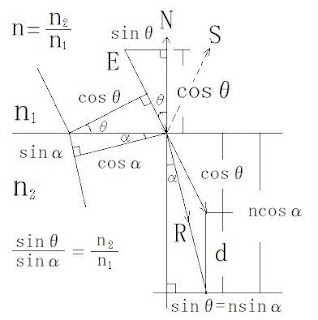
物質1から2へ光が進む時、物質1,2の絶対

屈折率をn₁、n₂、相対屈折率をn = n₁₂ = n₂/n₁

とし、入射光E,屈折面の法線N、反射光S、

屈折光Rとする

|E|=|N|=|R|=1

図5 屈折光R = (1/n)(E - d N)

 

光が当たった部分の長さを1にして

幅のある光が屈折する様子を書いた

のが図5です

 

物質1 : 物質2 = sinθ : sinα は、

単位時間当たりの光が進む距離の比

つまり、進みやすさの比です。

屈折率n₁, n₂は光の進みにくさなので

進みやすさの比は、

sinθ : sinα = n₂ : n₁ = n : 1

sinθ = nsinα

 

よって、図5の角αを持つ2つの

直角三角形は大が小のn倍になって

いる

 

R’= E - d Nと置くと、

R  = (1/n)R’

   = (1/n)(E - d N)

 

となり、dを求める、

 

d = ncosα - cosθ

ncosα = n√(1-sin²α) = √{n²-(nsinα)²}

= √(n²-sin²θ) = √{n²-(1-cos²θ)}

d = √{n²-(1-cos²θ)} - cosθ

 

屈折光Rと前回やった反射光Sは

R = (1/n)[E-[√{n²-(1-cos²θ)}-cosθ]N]

ただし、cosθ= -E･N

S = E+(2cosθ)N = E - 2(E･N)N

 

次に、入射光が屈折光(1-k)と反射光kに

分かれる割合

反射率k =

[ {sin(θ-α)/sin(θ+α)}² 

+ {tan(θ-α)/tan(θ+α)}² ] / 2

を、加法定理等で変形します

 

sin(θ-α)/sin(θ+α)

= (sinθcosα-cosθsinα)

/ (sinθcosα+cosθsinα)

= (nsinαcosα-cosθsinα)

/ (nsinαcosα+cosθsinα)

= {sinα(ncosα-cosθ)}

/ {sinα(ncosα+cosθ)}

= (ncosα-cosθ)/(ncosα+cosθ)

 

tan(θ-α)/tan(θ+α)

= {sin(θ-α)cos(θ+α)}

/ {cos(θ-α)sin(θ+α)}

= {(ncosα-cosθ)(cosθcosα-sinθsinα)}

/ {(cosθcosα+sinθsinα)(ncosα+cosθ)}

= (ncosαcosθcosα-ncosαsinθsinα

-   cosθcosθcosα+ cosθsinθsinα)

/ (ncosαcosθcosα+ncosαsinθsinα

+   cosθcosθcosα+ cosθsinθsinα)

= (ncosαcosθcosα- cosαsinθsinθ

-   cosθcosθcosα+ncosθsinαsinα)

/ (ncosαcosθcosα+ cosαsinθsinθ

+   cosθcosθcosα+ncosθsinαsinα)

= (ncosθ-cosα-cosα+ncosθ)

/ (ncosθ+cosα+cosα+ncosθ)

= (2ncosθ-2cosα)/(2ncosθ+2cosα)

= (n²cosθ-ncosα)/(n²cosθ+ncosα)

 

よって、k

= [ {sin(θ-α)/sin(θ+α)}² 

+   {tan(θ-α)/tan(θ+α)}² ] / 2

= [ {( ncosα- cosθ)/( ncosα+ cosθ)}² 

+   {(n²cosθ-ncosα/(n²cosθ+ncosα)}² ] / 2

以下、まとめ

 

c = -E･N = cosθ

S = E + (2c)N

もし c < 0 なら c = -c, n = 1/n, N = -N

 

a = n²-(1-c²)

もし a < 0 なら全反射(k = 1)で以下無効

 

b = √(a) = √{n²-(1-c²)} (= ncosα)

R = (1/n){E - N(b - c)}

k = (1/2)[ {(b-c)/( b+c)}²+{(n²c-b)/(n²c+b)}² ]

 

以上、反射と屈折を再帰的に呼び出し描画

します

 

NL-BASICとblg～.zip(ray008.bas)は

以下のリンクからダウンロードできます

NL-BASIC(N88-BASIC互換?)ホームページ

Readme.txtを読んで遊んで下さい

今回で終了です