N88-BASICで振り子 (2回目)
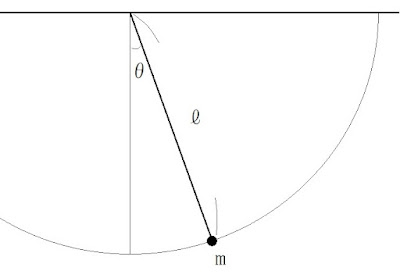
2023/12/26(火) N88-BASICで振り子 (2回目) 単振り子 (Simple pendulum) ■ 前提 https://ulprojectmail.blogspot.com/2023/12/pendulum-2.html 振り子 (2回目) より ▼ 定義 ℓ :紐の長さ(m) m :質点の質量(kg) θ:鉛直下方向からの角度(rad) g :重力加速度 ω:角速度(rad/s) f :振動数(Hz) A :振幅(m) B :位相(rad) ▼ 微分方程式 θ ( ・・ ) = -(g/ℓ)sinθ ▼ 近似式 sinθ≒θ (|θ| << 1)の時 2πf = ω = √(g/ℓ) θ = Acos(ωt+B) ▼ 近似式(初期角度が最大角の時) θ 0 :初期角度(最大角とする) 2πf = ω = √(g/ℓ) θ = θ 0 cos(ωt) θ ( ・ ) = -θ 0 ωsin(ωt) θ ( ・・ ) = θ 0 ω 2 cos(ωt) ■ 動作 離す角度を入力し 数値計算の振り子(黄色) (積分 θ ( ・ ) =∫ θ ( ・・ ) dt等は長方形近似で計算しています) と 近似式の振り子(水色) … (高校物理) を表示します ■ PC-8801 1070 VSYNC = &HA0 '--- &HA0:PC-98 , &H40:PC-88 を 1070 VSYNC = &H40 '--- &HA0:PC-98 , &H40:PC-88 に変更するとPC-8801用になります VL,NL,XL-BASICと blg~.zip (pend00 2 .bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい