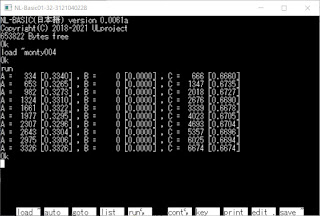
N88-BASICでゼノンの矢 (2回目) (アキレスと亀)

2021/12/27(月) N88-BASICでゼノンの矢 (2回目) 似たような問題 アキレスと亀のパラドックス (Achilles and the turtle paradox) 亀はアキレスより100m先から出発 1. 速い2m/sのアキレスでも今亀がいる所まで行くのに時間がかかる 2. その時間の間に遅い1m/sの亀でも少しは前に進む 1. 速い2m/sのアキレスでも今亀がいる所まで行くのに時間がかかる 2. その時間の間に遅い1m/sの亀でも少しは前に進む ・ ・ 1.2.を永遠に繰返してもアキレスは亀に追付けない??? 実際は、アキレスと亀の速度差は1m/sなので、 100m÷1m/s = 100秒後に追付くはず... ということで、 BASICで、この1.2.を繰返すと、 アキレスと亀の差と、経過時間が どう変化するかを計算して見ました 結果を見てみると、アキレスと亀の距離の差は0(m)に 近付き、経過時間は100(s)(追い付く時間)に近付いて いますつまり、1.2.を永遠に繰り返しても、時間は 100(s)に到達しない事が分かります つまり、1.2.を繰返すことは、追い付くまでの 事を永遠に語っているだけだと分かります この図ではオレンジの線を永遠に繰り返しても、 100sに到達しない事が分かります (1回目は50sで亀がアキレスの少し前にいます) 結局、ゼノンの矢も、アキレスと亀も 無限回繰り返すと無限の時間が過ぎると 思い込んでいたために起きた矛盾です よく考えてみると、数学では無限級数やその和が ある値に収束する(無限大にならない) ことは良くあることでした NL-BASICとblg~.zip(zeno002.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい