投稿

10月, 2022の投稿を表示しています

N88-BASICでアボガドロ定数

イメージ
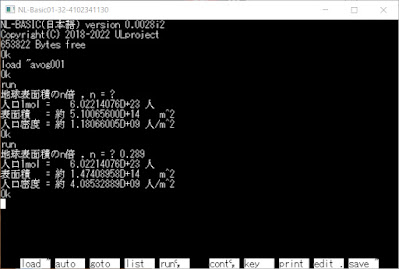
2022/10/26(水) N88-BASICでアボガドロ定数   アボガドロ定数( Avogadro constant )は N A  = 6.02214076×10 23  /mol (2019/5/20～)   1mol当たり 6022垓1407京6000兆0000億0000万0000   1mol = 6.02214076×10 23 個の水(分子)は コップ1/10(約18mL)程度なので 大して多くないように思えます   (分子量H 2 O≒18より約18g/mol、密度約1g/cm 3 、 として1cm 3 =1mLなので18mL/mol)     地球の表面積を使用して1molの大きさを 実感して見ます   世界人口を1mol人とすると 人口密度は何人/m 2  になるか   地球の表面積 5.100656×10 14  m 2  (陸と海全てを含む)   プログラムでは地球表面積の何倍かを 入力して1mol人の人口密度を表示します (Enterのみの入力で1倍になります)   6.02214076×10 23  / 5.100656×10 14  で 約10億人/m 2     住めません 1molは やはり多いです   地球表面積の約28.9%が陸地だそうですので 0.289を入力すると陸地のみの人口密度を 表示できます   約40億人/m 2       BASICの指数表記は □×10 △  を □E+ △ または □D+ △と書きます (Eは単精度、Dは倍精度)   N88-BASIC互換?VL,NL,XL-BASICと blg～.zip(avog001.bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  
続きを読む

N88-BASICで回転楕円体 (3回目)

イメージ
2022/10/20(木) N88-BASICで回転楕円体 (3回目)   地球を扁平楕円体で近似する 公称赤道半径R eE (N ominal equatorial Earth R adius ) 公称極　半径R pE (N ominal polar       Earth R adius ) R eE  = 6378.137×10 3 m R pE  = 6356.752 ×10 3 m   前回 https://ulprojectmail.blogspot.com/2022/10/n88-basicspheroid-2.html N88-BASICで回転楕円体 (2回目) より   扁平回転楕円体面(長半径a,短半径b) x 2 /a 2  + y 2 /b 2  = 1をx軸で回転 x 2 /a 2  + y 2 /b 2  + z 2 /a 2  = 1   体積　　V = (4/3)πab 2   表面積　S = 2πb{(a 2 /c)ln{(b+c)/a} + b} 焦点距離c = √(b 2 -a 2 ) (a＜b)   北極方向をx軸とし、a = R eE 、b = R pE  とする   N88-BASIC互換?VL,NL,XL-BASICと blg～.zip(sphe003.bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  
続きを読む

N88-BASICで回転楕円体 (2回目)

イメージ
2022/10/12(水) N88-BASICで回転楕円体 (2回目)   扁平回転楕円体面 (短半径a,長半径b) x 2 /a 2  + y 2 /b 2  = 1をx軸で回転 x 2 /a 2  + y 2 /b 2  + z 2 /b 2  = 1 について   前回 https://ulprojectmail.blogspot.com/2022/10/n88-basicspheroid-1.html N88-BASICで回転楕円体 (1回目) より   扁平回転楕円体面 (短半径a,長半径b) x 2 /a 2  + y 2 /b 2  + z 2 /b 2  = 1 で囲まれた体積は (4/3)πab 2   となる   扁平楕円体面の表面積 S S = 2πb{(a 2 /c)ln{(b+c)/a} + b} 焦点距離 c = √(b 2 -a 2 ) (a＜b) を求める   楕円 x 2 /a 2  + y 2 /b 2  = 1 を x軸周りに回転させて 楕円体を作ると考える   焦点距離 c = √|a 2 -b 2 | c 2  = a 2 -b 2  (a＞b) c 2  = b 2 -a 2  (a ＜ b)   回転体の半径 yは x 2 /a 2  + y 2 /b 2  = 1より y = f(x) = √{b 2 (1 - x 2 /a 2 )} y 2  = b 2 (1 - x 2 /a 2 )   y' = f'(x)とし x 2 /a 2  + y 2 /b 2  = 1の両辺をxで微分すると 2x/a 2  + 2yy'/b 2  = 0 yy' = -b 2 x/a 2   (yy') 2  = b 4 x 2 /a 4     y 2 +(yy') 2  = b 2 (1 - x 2 /a 2 ) + b 4 x 2 /a 4   = b 2 (1 - x 2 /a...
続きを読む

N88-BASICで回転楕円体 (1回目)

イメージ
2022/10/10(月) N88-BASICで回転楕円体 (1回目)   回転楕円体面 (フットボール形)(長半径a,短半径b) x 2 /a 2  + y 2 /b 2  = 1をx軸で回転 x 2 /a 2  + y 2 /b 2  + z 2 /b 2  = 1 について   楕円体の体積   https://ulprojectmail.blogspot.com/2021/08/vl-basic-1.html VL-BASICで結晶格子 (1回目) より半径 rの球の体積は(4/3)πr 3 　   なので半径 1の球(単位球)の体積は(4/3)π   径 a,b,cの楕円体は単位球をa,b,c方向に それぞれ a,b,c倍にしたものなので体積は (4/3)πabc となる   回転楕円体面 (長半径a,短半径b) x 2 /a 2  + y 2 /b 2  + z 2 /b 2  = 1 で囲まれた体積は (4/3)πab 2   となる     球の表面積   半径 rの球の体積を半径の関数V(r)とすると V(r) = (4/3)πr 3 　 V-rグラフの傾きはrの増加に対するVの 増加分なので半径 rでの表面積を表して いるので Vをrで微分して傾きを求めると 球の表面積 S = (d/dr)V(r) = 4πr 2 　     回転体の表面積 S y = f(x) [x=a～b] を x軸周りに回させると x～x+dx間のyの変化をdyとし 斜辺の長さは √(dx 2 +dy 2 ) = √{1+(dy/dx) 2 } dx = √(1+y' 2 ) dx これに円周の長さを掛けて 2πy√(1+y' 2 ) dxを x～x+dx間の表面積の近似とすると S = 2π∫y√(1+y' 2 ) dx [x=a～b] = 2π∫√{y 2 +(yy') 2 } dx [x=a～b]     楕円体面の表面積 S S = 2πb{(a 2 /c)tan -1 (c/b) + b} 焦点距離 c = √(a 2 -b 2 ) (a＞b) を...
続きを読む