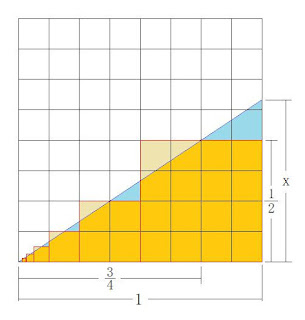
N88-BASICでアナログ時計
2021/11/28(日) N88-BASICでアナログ時計 アナログ時計を表示しました 1,2キーで秒針の動きを変える事が出来ます 1秒毎に動かすのは簡単です N88-BASICでは1秒以下の時間を計る関数が ありませんので、滑らかに動かすのは大変です そこで、1秒間で何回針を書き換えられるかを 測定し、1回の書き換えで進むべき時間を求め る事で滑らかに動かしています 余談 AM/PMを使った12時間表示では AM(午前)は00:00~12:00未満 PM(午後)は12:00~24:00未満 なので AM(午前)12:00が00:00(夜) PM(午後)12:00が12:00(昼) ですが 日本の明治?からの法律では 午前は01時0~12時 午後は13時0~24時 となっていて 午後12:00が00:00(夜) 午前12:00が12:00(昼) という事になっています つまり昼の12:30は午前という 大変混乱する法律を 未だに使っているのです 12:00は午前12:00で 12:01は午後12:01という解釈は 更に混乱を呼びます またアナログ時計に存在しない 午後0時などという更に混乱を 招く解釈をする方がいらっしゃいますが 初めに紹介したAM/PMのに解釈すれば すっきりするのだから 解釈を捻じ曲げて現行法を擁護するより 法律の方を変えるほうがすっきりすると 思います 現在ほとんどの方が 昼の12時から午後だという 認識をしていると思いますので (現行法では昼の12時は午前) 早く法改正すべきだと思います NL-BASICとblg~.zip(clock001.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい