科学,数学,趣味でPC © ULproject

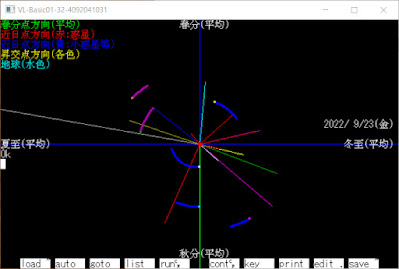
2022/9/23(金) VL-BASICで惑星の軌道 (2回目)   前回 https://ulprojectmail.blogspot.com/2022/09/vl-basic-1.html VL-BASICで惑星の軌道 (1回目) のプログラムを 途中で x軸(横軸)回りに視点を回転可能にしました 春分秋分などの表示文字の回転は非対応です   2022年9月23日(金) の秋分の日の惑星の位置 までを 1年前から表示しました   惑星の 点は手前で大きく、奥で小さく表示しています 軌跡の色と惑星の色は以下の通りです   青軌跡 (惑星) 白　 :水星 黄　 :金星 水色 :地球 紫　 :火星   紫軌跡 (小惑星) 黄　 :竜宮 緑　 :糸川   その他の惑星や彗星は 2:～冥王星 を選ぶと表示範囲に入ります 表示色などは DATA文を見て下さい 0黒 1青 2赤 3紫 4緑 5水 6黄 7白 8+色は軌跡が紫、色のみは軌跡が青 です   操作方法 '@'キーで自分が上方向へ移動 ':'キーで自分が下方向へ移動 enterキーで真上へ移動     遅いのでキーの押しすぎに注意して下さい   表示される軌道と実際の軌道に ズレがある場合があります 自己責任で使用して下さい (最新の軌道データを使用すると改善されるか もしれません)   VL-BASICとblg～.zip(plan002v.bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2022/9/21(水) VL-BASICで惑星の軌道 (1回目)   https://ulprojectmail.blogspot.com/2021/10/n88-basic-2.html N88-BASICで天体の軌道 (2回目) のプログラムを N88-BASIC互換?VL-BASICの 拡張命令 (ブロックIF文や行列関係の命令)を 使用して書き直し   2022年9月23日(金) の秋分の日の惑星の位置を表示 しました   青軌跡 白　 :水星 黄　 :金星 水色 :地球 紫　 :火星   紫軌跡 黄　 :竜宮 緑　 :糸川   表示される軌道と実際の軌道に ズレがある場合があります 自己責任で使用して下さい (最新の軌道データを使用すると改善されるか もしれません)   VL-BASICとblg～.zip(plan001v.bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2022/9/18(日) 命題が正しいのに対偶が正しくない パラドックス   ネットで見つけた問題を考えて見ました (2019/9に書いたリニューアル記事です)     問題   命題 :「注意されない ならば 私語をする」 が正しいなら 対偶 :「私語をしない ならば 注意される」 は正しい   　　　 ...正しくない気がする   　　　 何故か ?     前提   (論理) 命題 :「A なら　　　 B である」 が正しいなら 逆　 :「B なら　　　 A である」 は間違い 否定 :「A でないなら B でない」 は間違い 対偶 :「B でないなら A でない」 は正しい   (例) 命題 :「りんご なら 　　　果物 　である」 が正しいなら 逆　 :「果物　 なら 　　　りんご である」 は間違い 否定 :「りんご でないなら 果物　 でない」 は間違い 対偶 :「果物　 でないなら りんご でない」 は正しい   (問題) 命題 :「注意されない ならば 私語をする　」 が正しいなら 否定 :「注意される 　ならば 私語をしない」 は間違い 　　　 (注意されても私語をするかも) 逆　 :「私語をする　 ならば 注意されない」 は間違い 　　　 (私語をすると注意されるかも) 対偶 :「私語をしない ならば 注意される　」 は正しい?     考察   時系列をはっきりさせる   この命題の場合、注意という過去のアクションに対して 私語の現在のアクションが決まるという時系列で考えると   命題 :「注意されない(過去) ならば 私語をする(現在)」 　　　が正しいなら 対偶 :「私語をしない(現在) ならば 注意される(過去)」 　　　は、現在私語をしていない ならば 過去に注意された 　　　という事になり、正しい事が分かります   　　　勝手に現在と過去を入れ替えて 　　　私語をしていないのに注意されるという 　　　誤解をしたためパラドックスに感じたという事です     おまけ   命題 :「注意されない(過去) ならば 私語をする(現在)」 に...

2022/8/15(木) N88-BASICでネイピア数 (4回目)   ネイピア数e(Napier's constant)   e x  = lim[n→∞] (1 + x/n) n   を変形する   (a + b) n  = Σ n C i a n-i b i  [i = 0～n] と nCr = n(n-1)…(n-r+1)/r! より   (1 + x/n) n   = Σ n C i (x/n) i  [i = 0～n] = 1 + n (x/n) + n(n-1)/2! (x/n) 2   + n(n-1)(n-2)/3! (x/n) 3  + …   = 1 + x + (n-1)/2! (x/n) + (n-1)(n-2)/3! (x/n) 2  + … = 1 + x + (n-1)/2! (x/n) + (n 2 -3n+1)/3! (x/n) 2  + … = 1 + x + {1/2! - 1/(2!n)}x 2   + {1/3! - 3/(3!n) + 1/(3!n 2 )}x 3  + …   = 1 + x + x 2 /2! + x 3 /3! + … (n→∞) = x 0 /0! + x 1 /1! + x 2 /2! + x 3 /3! + … (n→∞)   lim[n→∞] (1 + x/n) n   = Σ(1/k!)x k  [k = 0～∞]   結果 e x  = lim[n→∞] (1 + x/n) n  = Σ(1/k!)x k  [k = 0～∞]   プログラムではmを入力し e x  = lim[n→∞] (1 + x/n) n  ≒ Σ(1/k!)x k  [k = 0～m] の計算結果を表示しています     追記 e x  はexp(x)とも表記し BASICではexp(x)を使用しa x はa^xと記述します     VL,NL,XL-BASICとblg～.z...

2022/9/12(月) N88-BASICでネイピア数 (3回目)   ネイピア数e(Napier's constant)   年利x (100x %) の利息について、1年をn等分して 複利で1年後の残金が何倍になるかを計算すると   n = 1 → 1+x n = 2 → (1+x/2)(1+x/2) = (1+x/2) 2   となるのでn等分の場合 (1 + x/n) n  倍になる   https://ulprojectmail.blogspot.com/2022/09/n88-basicnapier-1.html N88-BASICでネイピア数 (1回目) より e = lim[n→∞] (1 + 1/n) n   を使用して lim[n→∞] (1 + x/n) n   をeで表す   n/x = hと置くとn→∞のときh→∞ n = xhなので lim[n→∞] (1 + x/n) n   = lim[h→∞] (1 + 1/h) hx   = { lim[h→∞] (1 + 1/h) h  } x   　ここで「lim[n→∞] (1 + 1/n) n  = e」より = e x   となる   プログラムではnを入力し a = (1 + x/n) n  をe x  = exp(x)と共に 表示しています     ちなみに   10日で1割ならば1年(複利)で33倍近くになり 1日で1％ならば1年(複利)で38倍近くになります   年利x=0.1/10×365=3.65, 分割n=365/10=36.5 年利x=0.01×365  =3.65, 分割n=365で、それぞれ 32.42149286353205 37.78343433288728 と表示されます     より正確に計算するならば 現在のカレンダーに使用されている暦(グレゴリオ暦) の1年を近似した365.2425日を使用して下さい   グレゴリオ暦については https://ulprojectmail.blogspot.com/2...

2022/8/9(金) N88-BASICでネイピア数 (2回目)   ネイピア数e(Napier's constant)   e = lim(n→∞) (1 + 1/n) n   を変形する   二項定理と組合せは https://ulprojectmail.blogspot.com/2021/07/vl-basic3-1.html VL-BASICで3乗の展開の図 (1回目) https://ulprojectmail.blogspot.com/2021/11/n88-basicpc.html N88-BASICで順列組合せ を参照   (a + b) n  = Σ n C i a n-i b i  [i = 0～n] と nCr = n(n-1)…(n-r+1)/r! より   (1 + 1/n) n   = Σ n C i (1/n) i  [i = 0～n] = 1 + n (1/n) + n(n-1)/2! (1/n) 2   + n(n-1)(n-2)/3! (1/n) 3  + …   = 1 + 1 + (n-1)/2! (1/n) + (n-1)(n-2)/3! (1/n) 2  + … = 1 + 1 + (n-1)/2! (1/n) + (n 2 -3n+1)/3! (1/n) 2  + … = 1 + 1 + {1/2! - 1/(2!n)} + {1/3! - 3/(3!n) + 1/(3!n 2 )} + …   = 1 + 1 + 1/2! + 1/3! + … (n→∞) = 1/0! + 1/1! + 1/2! + 1/3! + … (n→∞)   e = lim[n→∞] (1 + 1/n) n   = Σ1/k! [k = 0～∞]   プログラムではmを入力し e = lim[n→∞](1 + 1/n) n  ≒ Σ1/k! [k = 0～m] で計算した結果を表示しています     おまけ ln xの微分(ln x = log e x)   f(x) = log e x、f'(x) = (d/d...

2022/9/6(火) N88-BASICでネイピア数 (1回目)   ネイピア数e(Napier's constant)   Ⅰ. 年利1(100%)の利息について、1年をn等分して 複利で1年後の残金が何倍になるかを計算すると   n = 1 → 1+1 = 2倍 n = 2 → (1+1/2)(1+1/2) = (3/2) 2  = 9/4   = 2.25倍 となるので (1 + 1/n) n  倍になる   n=3 → (1 + 1/3) 3  = (4/3) 3  =     64/   27 ≒ 2.37倍 n=4 → (1 + 1/4) 4  = (5/4) 4  =    625/  256 ≒ 2.44倍 n=5 → (1 + 1/5) 5  = (6/5) 5  =   7776/ 3125 ≒ 2.48倍 n=6 → (1 + 1/6) 6  = (7/6) 6  = 117649/46656 ≒ 2.52倍 … n=∞にした時の倍率をeとすると e = lim[n→∞] (1 + 1/n) n   よってeはネイピア数となる(Ⅱを参照)   プログラムでは、nを入力し a = (1 + 1/n) n  とネイピア数e=exp(1)を 表示しています     Ⅱ. f(x) = a x 、f'(x) = (d/dx)f(x)として f'(x) = f(x)となるaをeとすると   f'(x) = lim[h→0] {f(x+h)-f(x)}/h = lim[h→0] (a x+h  - a x )/h = a x  lim[h→0] (a h  - 1)/h = a x  より lim[h→0] (a h  - 1)/h = 1 lim[h→0] (a h  - 1) = lim[h→0] h lim[h→0] a h  = lim[h→0] (1 +...

2022/9/3(土) N88-BASICでパロンドのパラドックス   パロンド(Parrondo)のパラドックスとは 不利なゲームを組合わせているのに 有利なゲームができるというものだそうです   ゲームA(不利なゲーム) 　48%の確率で1円得、52%の確率で1円払う   ゲームB(不利なゲーム) 　所持金が3の倍数なら 　　 1%の確率で1円得、99%の確率で1円払う 　所持金が3の倍数以外なら 　　85%の確率で1円得、15%の確率で1円払う   ゲームC(有利なゲーム) 　半々の確率でゲームAまたはゲームBをする   これら、ゲームA～Cの期待値を求めて見ます まず、 p a  = 0.48 p b0  = 0.01 p b1  = 0.85 p c  = 0.5 と置いて、式をつくります   ゲームA 　p a の確率で1円得、1-p a の確率で1円払う   ゲームB 　所持金が3の倍数なら 　　p b0 の確率で1円得、(1-p b0 )の確率で1円払う 　所持金が3の倍数以外なら 　　p b1 の確率で1円得、(1-p b1 )の確率で1円払う   ゲームC 　p c の確率でゲームA、(1-p c )の確率でゲームBをする   期待値E BC   所持金を3で割った余りが0,1,2である確率を それぞれx,y,zとし、 余りが0の時、勝つ確率をp 0 、それ以外の時、 勝つ確率をp 1 とする   所持金/3の余り:確率 0(x)→1(y,+1):p 0 、0(x)→2(z,-1):(1-p 0 ) 1(y)→2(z,+1):p 1 、1(y)→0(x,-1):(1-p 1 ) 2(z)→0(x,+1):p 1 、2(z)→1(y,-1):(1-p 1 )   x = (1-p 1 )y + p 1 z (y→x,z→x) y = (1-p 1 )z + p 0 x (z→y,x→y) z = (1-p 0 )x + p 1 y (x→z,y→z) x + y + z = 1   z + y = 1 - x 期待値E BC = {1円×p 0 -1円×(1-p 0 )}･x　　　…...

2022/9/1(木)   緑色の目をしたドラゴンの問題（Green-eyed dragons ) を100匹から3人にするなど多少アレンジした問題です   目の色が緑か赤のどちらかだと知らされている 緑目の3人A,B,Cが居る島があり、3人共次の条件がある   1. 他人の目の色は見る事が出来る 2. 自分の目の色を自身の思考以外で知る事は出来ない 3. 自分の目の色が分った時は、その日のうちに島を出る ある日(1日目)に島にやってきた旅人が 「この島人3人の内、少なくとも1人は緑目だ」 と言って去っていった 全員が島を去るのは何日目か                     1日目   緑目〇,赤目×、A,B,Cの思考をそれぞれ□,吹出,くも吹出とする (Aは、Bが「Cは全員が×の可能性を 否定できない 」と考えている、 と考えているが、旅人の一言で 否定できる 様になる)   Aの思考の中のBの思考の中のCの思考では A,B共に×ならCが〇なのでCは出ていくとAは考える Aの思考の中のCの思考の中のBの思考では A,C共に×ならBが〇なのでBは出ていくとAは考える   しかし、現実は全員〇なのでCもBも出ていかない (B,CもAと同じことを考えている)   2日目 B,C共出ていかなかったので、A,B共に×、A,C共に×は無しになる   Aの思考の中のBの思考ではB,Aの少なくとも1人は〇と考える のでAが×ならBは〇と分かりBは出ていくとAは考える Aの思考の中のCの思考ではC,Aの少なくとも1人は〇と考える のでAが×ならCは〇と分かりCは出ていくとAは考える   しかし、現実は全員〇なのでBもCも出ていかない (B,CもAと同じことを考えている)       3日目 B,C共出ていかなかったので、 Aは自分が×ではないので〇だと分かり出ていく   B,CもAと同じことを考えているので全員出ていく   答え、3日目(旅人が来てから2日後)に全員出ていく   人数が1人なら1日目に、2人なら2日目に出ていく 3人な...