ULprojectのホームページ © ULproject

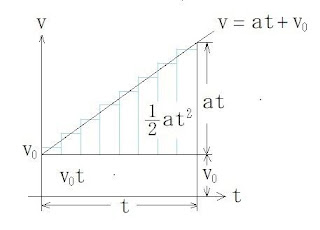
2021/8/18(水) N88-BASICでゲーム (2回目) by ULproject 1. 斜方投射で的方向に投なげる (モンキーハンティング) (発射と同時に的を落とすとあたる) 2. 的にあたるように投げる(低い軌道) 3. 的にあたるように投げる(高い軌道)   の3通りを1～3キーで選び的にあてるゲームです   ターゲットは1/2の確率で落ちます よって、1/2の確率で当たるゲーム です 投げ方は3通りですが、当たる確率は1/2です 何かパラドックスが作れそうですね   以下、式の説明です   以後ベクトルを大文字、その他は小文字にします   加速度A = const.(一定)、 速度V、初速度V 0 、 位置P、初期位置P 0   時間t、微小時間dt とすると、   速度の微小増分dV = Adt (速度の増分=加速度×時間は微小時間 なら加速度一定でなくても成り立つ) dV/dt = Aとすると、 Vの時間微分がAと分かる。   両辺tで積分すると ∫dV/dt dt = ∫Adt ∫dV = ∫Adtは、A = const.なので、 V = At + C ここでt=0のときV=V 0 なので、 V 0  = C よって、 V = At + V 0     位置の微小増分dP = Vdt (位置の増分=速度×時間は微小時間 なら速度一定でなくても成り立つ) dP/dt = Vとすると、 Pの時間微分がVと分かる。   両辺tで積分すると ∫dP/dt dt = ∫Vdt ∫dP = ∫Vdt P = ∫ At+V 0  dt   = (1/2)Att + V 0 t + C ここでt=0のときP=P 0 なので、 P 0  = C よって、 P = (1/2)At 2  + V 0 t + P 0   図1. 速度と時間のグラフ   速度と時間のグラフv - at + v 0 の 傾きaが加速度(一定の場合)で、 面積(1/2)at 2  + v 0 tが移動距離になります   三角形の部分が分かりにくいときは 水色の長方形が各時間の間の移動距離 になりますので、三角形の面積と一緒に なります 等加速度運動(加速度一定の運動)の場合 初速と最高速の平均速度で移動したのと 同じ距離移動します   傾きを求めるのが微分で、面が積分です   まとめ A

2021/8/16(月) N88-BASICでゲーム  (1回目) by ULproject   球同士の衝突と跳返り   大文字ベクトル、小文字スカラー 文字の後の、 'は衝突後、数字は球番号   球同士の反発係数、衝突面に水平 ,垂直u,e 球の中心位置 P,半径r,質量m,速度V 衝突面の球 1方向の法線N = (P 1 -P 2 )/|P 1 -P 2 |   球同士の衝突は、 |P 1 -P 2 | ≦ r 1 +r 2   なので √{(P 1 -P 2 )･(P 1 -P 2 )} ≦ r 1 +r 2   (P 1 -P 2 )･(P 1 -P 2 ) ≦ (r 1 +r 2 )(r 1 +r 2 ) で判断できます。   ここで、ベクトルの計算ですが、 P(i) (i=0,1,2) をPのx,y,z成分と すると、 P = P 1  - P 2 は、 P(i) = P1(i) - P2(i) (i=0,1,2) P･Pは ΣP(i)P(i) (i=0,1,2) となります   BASICでは、 P(0) = P1(0) - P2(0) P(1) = P1(1) - P2(1) P(2) = P1(2) - P2(2) D = P(0)*P(0)+P(1)*P(1)+P(2)*P(2) R = R1 + R2 IF D <= R*R THEN 重なり又は接触 となります。   反発させるときは、球が接触している 間は再び反発しないようにしないと 球が離れなくなります。   次に反発についてですが、衝突面に 水平な成分は、球の回転に関係します が、ここでは球の回転は考えずに 垂直成分と同じように反発係数で 減速させる事にします。   衝突面に垂直な成分 (v 1 は球 1の速度、v 1 'は衝突後) 運動量 p = mv 運動量保存則 p 1 +p 2 =p 1 '+ p 2 'より p 1 +p 2  = m 1 v 1 '+ m 2 v 2 ' 反発係数 e = -(v 1 '- v 2 ')/(v 1  - v 2 )より ev 1  - ev 2  = -v 1 '+ v 2 '     em 2 v 1  - em 2 v 2  = -m 2 v 1 

2021/8/8(日) VL-BASICで結晶格子 (3回目)   六方最密構造   r:原子半径 a:単位格子のひし形の辺の長さ(2r) h:単位格子の柱の高さ   六方最密構造の単位格子は ひし形を底面とした四角柱で それが 3個集まると正六角柱となる 正六角形の辺の長さは c = 2r 高さは、正四面体の高さの 2倍となる   上図左の原子の上に中央図の 3つの原子 (太線)が乗っており、さらに左図の原子が 乗る３層構造を考える   右下図の 4つの原子の中心を結ぶと 正四面体になっている これが上下の層に存在するので、 正四面体 2個分の高さが 六角柱の高さとなる   1辺の長さがxの正四面体の高さyは y = √(2/3)x = {(√6)/3}x これを h = 2y , x = 2rに代入 h/2 = {(√6)/3}2r よって 単位格子の柱の高さ h = {(4√6)/3}r 正四面体の高さは 正四面体の重心 (原点とする)から 各頂点へのベクトルを A,B,C,Dとすると (以後大文字は位置ベクトルまたは 点の位置とする ) A,B,C,D方向の力は釣合う関係にある (A + B + C + D = 0ベクトル) ベクトル Dをz軸方向 ベクトル Aのz成分を0にしたベクトルを x軸方向にとると ベクトル A,B,Cのx成分の釣合いから Ax = |Bx| + |Cx| (Ax : Bx = Ax : Cx = 2 : 1)となるので 点 Dから△ABCへの垂線と△ABCの交点Hは △ABCの点から線分BCへの垂線を2:1に 内分する点となっている 線分 AH = △ABCの高さ×(2/3) = 線分AB{(√3)/2}x(2/3) = 線分AB(√3)/3   よって、正四面体の高さ DH(yとする)は 辺の長さ AB(xとする)を使って   x 2  = y 2  + {x(√3)/3} 2   y 2  = x 2  - (3/9)x 2  = (2/3) x 2   y = √(2/3)x = {(√6)/3}x と表せる   原子半径 r 単位格子のひし形の辺の長さ a = 2r 単位格子の柱の高さ h = {(4√6)/3}r   原点を A B方向をx軸 C方向をy軸 D方向をz軸とした 底辺 ABC頂点Dの正四面体構造の 半径 r