N88-BASICで命数法 (3回目)
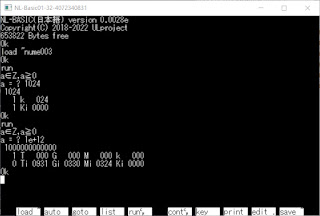
2022/7/30(土) N88-BASICで命数法 (3回目) 1024を 1 k 024 1 Ki 0000 x∈Zはxは整数という意味です 1k = 1000、1M = 1000 2 1Ki = 1024、1Mi = 1024 2 です VL,NL,XL-BASICとblg~.zip(nume003.bas)は 以下のリンク)からダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい



