コリオリ力 (4回目)
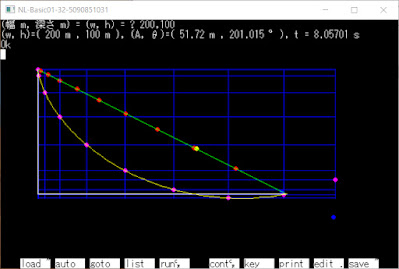
2023/9/28(木) コリオリ力 (4回目) (Coriolis force) 自由落下 ■ 前提 ▼ 定義 F :物体に加える力 F C :コリオリ力(Coriolis force) f C :遠心力(Centrifugal force) T:地球の自転周期[86164.098903691(s)] ω:地球の角速度[2π/T (rad/s)] G:重力定数[6.67430×10 -11 (Nm 2 /kg 2 )] M:地球質量[5.972×10 24 (kg)] R:地球の半径[6367.5×10 3 (m)北緯45°] g:重力加速度[g = GM/R 2 ≒ 9.83077(m/s 2 )] (北緯45°の標準重力加速度は正確にg n = 9.80665 m/s 2 ) h:高さ(m)[|h|<<|R|つまり|R+h|≒|R|とする) φ:北緯(rad)[日本の北緯35°, λ東経135°] (x, y, z) = (南, 東, 上)とする 原点(x, y, z) = (0, 0, R) ▼ 運動方程式 m a = m r ( ・・ ) = F + F C + f C = F - 2m ω × r ( ・ ) ' - m ω ×( ω × r ') = F - 2m ω × r ( ・ ) ' + mω 2 { r '- ω ( ω ・ r ')/ω 2 } = F - 2m ω × v ' + mω 2 r ' ⊥ = (0, 0, -mg) + (mω 2 Rcosφsinφ, 0, mω 2 Rcos 2 φ) + (2mω y ( ・ ) sinφ, -2mω( x ( ・ ) sinφ+ z ( ・ ) cosφ), 2mω y ( ・ ) cosφ) ■ 導出 ▼ 重力加速度(万有引力と遠心力による加速度) g = ( F + F C )/m = (0, 0, -GM/R 2 ) + (ω 2 Rcosφsinφ, 0, ω 2 Rcos 2 φ) ≒ (0, 0, -g n ) (重力加速度gを標準重力加速度g n で近似) a = r ( ・・ ) = ( F + F C + f C )/m =