ULprojectのホームページ © ULproject

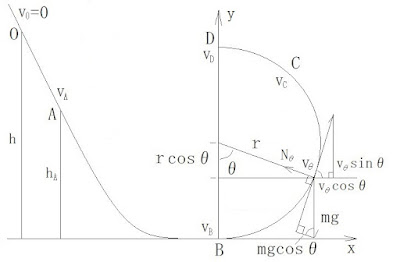
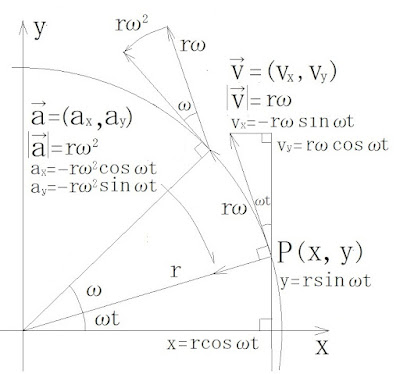
2023/3/30(木) N88-BASICで遠心力 (3回目)   ( Centrifugal force )   式など詳しくは https://ulprojectmail.blogspot.com/2023/03/centrifugal-3.html 遠心力 (3回目) を参照して下さい         図1.O→A→B→Cと移動する質量mの質点(Cは最終接地点) 　　その後の最高点をE,着地点をFとする 　　O→A→B→C→E→FまたはO→A→B→D→F     半円の半径rと離す高さhを入力すると   h ≧ h 0  = 5/2rの時 　B地点の速度vb 　D地点の速度vd 　F地点の位置(xf, 0 ) を表示 v D  = √{2g(h - 2r)}   h ＜ h 0  = 5/2rの時 　B地点の速度vb 　C地点の速度vc, (vcx,vcy), 角度θ=vcθ 　C地点の位置(xc, hc) 　E地点の位置(xe, he) 　F地点の位置(xf, 0 ) を表示 v B  = √(2gh) cosθ C  = (r - h C )/r sinθ C  = x C  / r h C  = (r + 2h)/3 (h C  = h if h ≦ r) x C  = √{r 2  - (r - h C ) 2 } v C  = √{2g(h - r) / 3} (v C  = 0 if h ≦ r) v C  = = (v Cx ,v Cy ) = (v C cosθ C ,v C sinθ C ) t 1  = v Cy /g h E  = h C  + v Cy 2 /(2g) x E  = x C  + v Cx t 1  = x C  + v Cx v Cy /g t 2  = √(2h E /g) x F  = x E  + v Cx t 2       ここでATN()は-π/2～π/2の関数なので (π/2=90ﾟ) tan(π/2-θ) = cosθ/sinθなので π/2-θ = ATN(cosθ/sinθ) θ = π/2 - ATN(cosθ/sinθ) として0～πを求めています     VL,NL,XL-BASICとblg～.zip(cent003.bas)は 以下のリンクからダウンロードできます https://ulpr

2023/3/27(月) 遠心力 (3回目)   ( Centrifugal force )   図1.O→A→B→C(→D)と移動する質量mの質点(Cは最終接地点) 　　その後の最高点をE,着地点をFとする 　　O→A→B→C→E→FまたはO→A→B→D→F     前回より x C  = √{r 2  - (r - h C ) 2 } cosθ C  = (r - h C )/r sinθ C  = x C  / r sinθ C  = (1/r)√{r 2  - (r - h C ) 2 } v C  = √{(v B 2  - 2gr) / 3} (v C  = 0 if v B 2  < 2gr) v C  = = (v Cx ,v Cy ) = (v C cosθ C ,v C sinθ C ) (方向は水平右方向からの仰角θ)       (1)O地点の高さhをv A とh A で表す 力学的エネルギー保存則より (1/2)mv A 2  + mgh A  = mgh h = h A  + v A 2 /(2g)       以後O地点の高さhを使用して表す   (2) h≧h 0 の時のD地点での速度v D   h 0  = (5/2)r h ≧ h 0 の時v B  ≧ √(5gr) v B  = √(2gh) 力学的エネルギー保存則より (1/2)mv B 2  = (1/2)mv D 2  + 2mgr v D 2  = v B 2  - 4gr v D  = √(2gh - 4gr) v D  = √{2g(h - 2r)}       (3) h≧h 0 の時の地面Fまでの時間t 2   2r = (1/2)gt 2 2   t 2  = √(4r/g)       (4)最終接地点の高さh C をhで表す  h C  = (gr + v B 2 )/(3g) = (gr + 2gh)/(3g)   h C  = (r + 2h)/3 (h C  = h if h ≦ r) … (力学的エネルギー保存則より)       以後h C を使用して表す   (5)離れてから最高点h E までの時間t 1   v C  = (v Cx ,v Cy ) = (v C cosθ C ,v C sinθ C ) なので v y  = v Cy  

2023/3/25(土) N88-BASICで遠心力 (2回目)   ( Centrifugal force )   式など詳しくは https://ulprojectmail.blogspot.com/2023/03/centrifugal-2.html 遠心力 (2回目) を参照して下さい     図1.O→A→B→Cと移動する質量mの質点(Cは最終接地点) 　　その後の最高点をE,着地点をFとする 　　O→A→B→C→E→FまたはO→A→B→D→F   D地点に到達する最小のhをh 0 とする 半径rを入力すると h 0 ,v B ,v D ,x F を表示する   h 0  = (5/2)r v B  = √(5gr) v D  = √(gr) x F  = -2r     VL,NL,XL-BASICとblg～.zip(cent002.bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい    

2023/3/19(日) 遠心力 (2回目)   ( Centrifugal force )     (1)垂直抗力N θ     図1.O→A→B→Cと移動する質量mの質点(Cは最終接地点) 　　その後の最高点をE,着地点をFとする 　　O→A→B→C→E→FまたはO→A→B→D→F     質点が角度θの位置のときの垂直抗力N θ を求める N θ  = 遠心力 + 地面に垂直な重力成分より N θ  = mv θ 2 /r + mgcosθ     ここで、力学的エネルギー保存則より (1/2)mv θ 2  + mgr(1-cosθ) = (1/2)mv B 2   v θ 2  = v B 2  - 2gr(1-cosθ)   N θ  = mv θ 2 /r + mgcosθ = [m{v B 2  - 2gr(1-cosθ)} + mgrcosθ]/r = m(v B 2  - 2gr + 2grcosθ + grcosθ)/r = (m/r)(v B 2  - 2gr + 3grcosθ) N θ  = mv B 2 /r + mg(3cosθ - 2)       (2)最終接地点の角度θ C   垂直抗力N θ ≧0の間接地しているので N θ  < 0となる直前の N θ  = 0となる角度を求める(θ C  >= 90ﾟ)   N θ  = mv B 2 /r + mg(3cosθ C  - 2) = 0 3cosθ C  - 2 = -v B 2 /(gr) 3cosθ C  = 2 - v B 2 /(gr) cosθ C  = (2gr - v B 2 )/(3gr) θ C  = Cos -1 {(2gr - v B 2 )/(3gr)}   因みに Cos -1 とTan -1 の変換 y = cosx、x = Cos -1 y z = tanx、x = Tan -1 z z = tanx = sinx/cosx = √{(1-cos 2 x) / cos 2 x} = √{(1-y 2 )/y 2 } = √(1/y 2  - 1) y < 0 if x > 90ﾟ       (3)最終接地点の高さh C   cosθ C  = (2gr - v B 2 )/(3gr) h C  = r(1-cosθ C

2023/3/12(日) N88-BASICで遠心力 (1回目)   ( Centrifugal force )   式など詳しくは https://ulprojectmail.blogspot.com/2023/03/centrifugal-1.html 遠心力 (1回目) を参照して下さい     半径r(m),速度r(m/s)を入力すると 遠心力F'(N)などが表示されます   1 kgfは地球上が質量1kgを引く力 (1kgを持つのに必要な力)です F = ma = mgよりm = F/g   VL,NL,XL-BASICとblg～.zip(cent001.bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2023/3/8(水) 遠心力 (1回目)   ( Centrifugal force )     (1)等速円運動     図 1.原点を中心とする半径rの円周上を点P(x,y)が 　　角速度ω(rad/s)で等速円運動をしている   時間をt(s)として θ(rad) = ωt x = rcosθ y = rsinθ   以下ベクトルaは太字斜め a で表すとし 点Pの位置ベクトルを r とする 図1より   r  = (x   ,y   ) = (rcosωt, rsinωt) v  = (v x ,v y ) = (-rωsinωt, rωcosωt) 　= (-ωy,ωx) a  = (a x ,a y ) = (-rω 2 cosωt, -rω 2 sinωt) 　= (-ω 2 x,-ω 2 y)   時間微分でも求める事ができる r  = (x   ,y   ) = (rcosωt, rsinωt) v  = d r /dt = r ( ・ )   = (ω･-rsinωt, ω･rcosωt) a  = d v /dt = v ( ・ )  = (ω 2 ･-rcosωt, ω 2 ･-rsinωt)       (2)速さv(速度の大きさ)と加速度の大きさa   r = | r  | = r  ･ r  = √(x 2  + y 2 ) v = | v  | = v  ･ v  = √{(-ωy) 2  + (ωx) 2 } = ω√(x 2  + y 2 ) = rω a = | a  | = a  ･ a  = √{(-ω 2 x) 2  + (-ω 2 y) 2 } = ω 2 √(x 2  + y 2 ) = rω 2         (3)向心力 F   質点Pの質量をm(kg）とする 点Pは常に中心方向へ加速度しているので 向心力 F  = m a の力を受けていることになる 向心力の大きさF = ma = mrω 2         (4)遠心力 F  '   質点Pが中心と反対方向に力を受けている と感じる見かけ上の力で 向心力とは大きさが同じで方向が逆となる 遠心力 F  '= -m a     遠心力の大きさF'= mrω 2   また v = rωよりω 2  = v 2 /r 2  なので   遠心

2023/3/1(水)   テセウスの船 ( Ship of Theseus )のパラドックス   ある船を老朽化した部品を新しい部品で修理して 交換した元の部品で同じ船を作っていく   始めの船(元の船の部品はない)と コピーした船(全て元の船の部品) の内どちらが本物か分からなくなる パラドックス   全て新しい部品でできているが やはり始めの船が本物といえるが   全て元の船の部品でできているから コピーした船の方が本物ともいえる   個人的解答 元の船(全て新しい部品)がオリジナルであり コピーした船(全て元の部品)はクローンだと 思います     考察(個人的見解)   人(自分や近しい人)で考えて見る   例えば、自分の身体は元の細胞が 新しい細胞に置き換わっていますが その元の細胞で自分のコピーを作ったとする   この場合、自分の意思は 新しい細胞でできた自分にあり   元の細胞でできた自分はクローンであり 意思は他人(自分ではない)であろうから   新しい部品で出来た元の船が本物であり 元の部品でつくられた船はクローンだと 考えます