三角関数 (1回目)
2021/9/27(月)
三角関数 (1回目)
加法定理
sin(α±β) = sinαcosβ±cosαsinβ
cos(α±β) = cosαcosβ ∓sinαsinβ
tan(α±β) = (tanα±tanβ)/(1 ∓tanαtanβ)
倍角公式
sin2θ = 2sinθcosθ
cos2θ = 1 - 2sin2θ = 2cos2θ - 1
tan2θ = 2tanθ/(1-tan2θ)
半角公式
sin2(θ/2) = (1 - cosθ) / 2
cos2(θ/2) = (1 + cosθ) / 2
tan2(θ/2) = (1 - cosθ) / (1 + cosθ)
三角関数は、原点Oが中心で半径rの
円周上の点をP(x,y)、正のx軸と
線分OPとのなす角をθとし、
sinθ = y / r
cosθ = x / r
tanθ = y / x
で定義される
(底辺x,高さy,斜辺r, xとrのなす角θの
直角三角形の辺の比を定義している)
x = rcosθ
y = rsinθ
は半径rの円を示している
BASICでは度数法の360°を2πとする、
弧度法(ラジアン)で計算されます
d°とtラジアンの変換は、
d = 180t / π
t = πd / 180
です
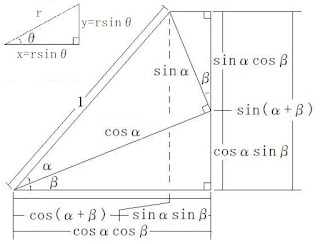
加法定理の導出
三角関数 (1回目)
加法定理
sin(α±β) = sinαcosβ±cosαsinβ
cos(α±β) = cosαcosβ ∓sinαsinβ
tan(α±β) = (tanα±tanβ)/(1 ∓tanαtanβ)
倍角公式
sin2θ = 2sinθcosθ
cos2θ = 1 - 2sin2θ = 2cos2θ - 1
tan2θ = 2tanθ/(1-tan2θ)
半角公式
sin2(θ/2) = (1 - cosθ) / 2
cos2(θ/2) = (1 + cosθ) / 2
tan2(θ/2) = (1 - cosθ) / (1 + cosθ)
三角関数は、原点Oが中心で半径rの
円周上の点をP(x,y)、正のx軸と
線分OPとのなす角をθとし、
sinθ = y / r
cosθ = x / r
tanθ = y / x
で定義される
(底辺x,高さy,斜辺r, xとrのなす角θの
直角三角形の辺の比を定義している)
x = rcosθ
y = rsinθ
は半径rの円を示している
BASICでは度数法の360°を2πとする、
弧度法(ラジアン)で計算されます
d°とtラジアンの変換は、
d = 180t / π
t = πd / 180
です
加法定理の導出
sin(α+β) = sinαcosβ+cosαsinβ
cos(α+β) = cosαcosβ-sinαsinβ
図1. 加法定理
sin(-β) = -sinβ
cos(-β) = cosβ
sin(α-β) = sinαcosβ-cosαsinβ
cos(α-β) = cosαcosβ+sinαsinβ
tan(α±β) = sin(α±β) / cos(α±β)
= (sinαcosβ±cosαsinβ)
/ (cosαcosβ∓sinαsinβ)
[分子分母をcosαcosβで割り
tanθ = sinθ/cosθで置き換える]
= (tanα±tanβ)/(1∓tanαtanβ)
倍角公式の導出
sin2θ = 2sinθcosθ
cos2θ = cos2θ - sin2θ = 1 - 2sin2θ
= 2cos2θ - 1
tan2θ = 2tanθ/(1-tan2θ)
半角公式の導出
cos2θ = 1 - 2sin2θ、2sin2θ = 1 - cos2θ
より
sin2(θ/2) = (1 - cosθ) / 2
cos2θ = 2cos2θ - 1、2cos2θ = 1 + cos2θ
より
cos2(θ/2) = (1 + cosθ) / 2
tan2(θ/2) = sin2(θ/2)/cos2(θ/2)
より
tan2(θ/2) = (1 - cosθ) / (1 + cosθ)