遠心力 (1回目)

2023/3/8(水)
遠心力 (1回目)
 
(Centrifugal force)
 
 
(1)等速円運動

 
 

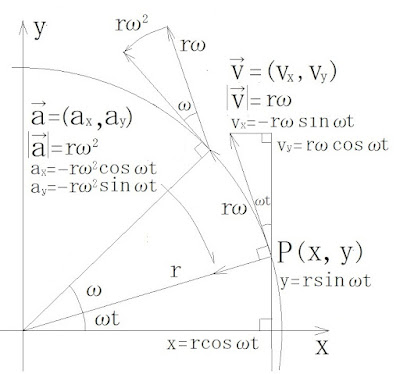
図1.原点を中心とする半径rの円周上を点P(x,y)が

　　角速度ω(rad/s)で等速円運動をしている
 
時間をt(s)として
θ(rad) = ωt
x = rcosθ
y = rsinθ
 
以下ベクトルaは太字斜めaで表すとし
点Pの位置ベクトルをrとする
図1より
 
r = (x ,y ) = (rcosωt, rsinωt)
v = (v_x,v_y) = (-rωsinωt, rωcosωt)
　= (-ωy,ωx)
a = (a_x,a_y) = (-rω²cosωt, -rω²sinωt)
　= (-ω²x,-ω²y)
 
時間微分でも求める事ができる
r = (x ,y ) = (rcosωt, rsinωt)
v = dr/dt = r(・) = (ω･-rsinωt, ω･rcosωt)
a = dv/dt = v(・) = (ω²･-rcosωt, ω²･-rsinωt)
 
 
 
(2)速さv(速度の大きさ)と加速度の大きさa
 
r = |r | = r ･r = √(x² + y²)
v = |v | = v ･v = √{(-ωy)² + (ωx)²}
= ω√(x² + y²) = rω
a = |a | = a ･a = √{(-ω²x)² + (-ω²y)²}
= ω²√(x² + y²) = rω² 
 
 
 
(3)向心力F
 
質点Pの質量をm(kg）とする
点Pは常に中心方向へ加速度しているので
向心力F = maの力を受けていることになる
向心力の大きさF = ma = mrω² 
 
 
 
(4)遠心力F '
 
質点Pが中心と反対方向に力を受けている
と感じる見かけ上の力で
向心力とは大きさが同じで方向が逆となる
遠心力F '= -ma 
 
遠心力の大きさF'= mrω² 
また
v = rωよりω² = v²/r² なので
 
遠心力の大きさF'= mrω² = mv²/r