遠心力 (2回目)

2023/3/19(日)
遠心力 (2回目)
 
(Centrifugal force)
 
 
(1)垂直抗力N_θ 

 

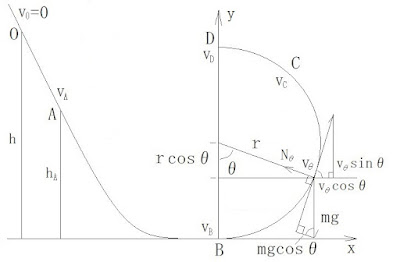
図1.O→A→B→Cと移動する質量mの質点(Cは最終接地点)
　　その後の最高点をE,着地点をFとする
　　O→A→B→C→E→FまたはO→A→B→D→F
 
 
質点が角度θの位置のときの垂直抗力N_θを求める
N_θ = 遠心力 + 地面に垂直な重力成分より
N_θ = mv_θ²/r + mgcosθ
 
 
ここで、力学的エネルギー保存則より
(1/2)mv_θ² + mgr(1-cosθ) = (1/2)mv_B² 
v_θ² = v_B² - 2gr(1-cosθ)
 
N_θ = mv_θ²/r + mgcosθ
= [m{v_B² - 2gr(1-cosθ)} + mgrcosθ]/r
= m(v_B² - 2gr + 2grcosθ + grcosθ)/r
= (m/r)(v_B² - 2gr + 3grcosθ)
N_θ = mv_B²/r + mg(3cosθ - 2)
 
 
 
(2)最終接地点の角度θ_C 
垂直抗力N_θ≧0の間接地しているので
N_θ < 0となる直前の
N_θ = 0となる角度を求める(θ_C >= 90ﾟ)
 
N_θ = mv_B²/r + mg(3cosθ_C - 2) = 0
3cosθ_C - 2 = -v_B²/(gr)
3cosθ_C = 2 - v_B²/(gr)
cosθ_C = (2gr - v_B²)/(3gr)
θ_C = Cos^-1{(2gr - v_B²)/(3gr)}
 
因みに
Cos^-1とTan^-1の変換
y = cosx、x = Cos^-1y
z = tanx、x = Tan^-1z
z = tanx = sinx/cosx = √{(1-cos²x) / cos²x}
= √{(1-y²)/y²}
= √(1/y² - 1)
y < 0 if x > 90ﾟ
 
 
 
(3)最終接地点の高さh_C 
cosθ_C = (2gr - v_B²)/(3gr)
h_C = r(1-cosθ_C)
= r{1 - (2gr - v_B²)/(3gr)}
= r(3gr - 2gr + v_B²)/(3gr)
h_C = (gr + v_B²)/(3g)
 
 
 
(4)最終接地点のB地点からの水平距離x_cをh_cで表す 
x_C = √{r² - (r - h_C)²}
 
 
 
(5)cosθ_Cとsinθ_Cをh_Cで表す
cosθ_C = (r - h_C)/r
sinθ_C = x_C / r
sinθ_C = (1/r)√{r² - (r - h_C)²}
 
 
 
(6)最終接地点の速度v_C 
N_θ = 0のときの速度の大きさv_Cは
v_C² = v_B² - 2gr(1-cosθ_C)と
cosθ_C = (2gr - v_B²)/(3gr)より
 
v_C² = v_B² - 2gr{1 - (2gr - v_B²)/(3gr)}
= v_B² + {-2gr + 2(2gr - v_B²)/3}
= (3v_B² - 6gr + 4gr - 2v_B²) / 3
= (v_B² - 2gr) / 3
v_C = √{(v_B² - 2gr) / 3} (v_C = 0 if v_B² < 2gr)
 
 
速度v_C は図1.より
v_C = (v_Ccosθ_C,v_Csinθ_C)
(方向は水平右方向からの仰角θ)
 
 
 
(7)最終接地点の角度がθ_Dの時の速度v_D 
(θ_D = 180ﾟ)
 
cosθ_C = (2gr - v_B²)/(3gr)
cosθ_D = cos180ﾟ = -1より
(2gr - v_B²)/(3gr) = -1
(v_B² - 2gr) = 3gr … (*)
 
v_B = √(5gr)
 
v_D = √{(v_B² - 2gr) / 3} … (*)を代入
= √{3gr / 3}
v_D = √(gr) … 水平負方向
 
 
 
(別解)
h_C = (gr + v_B²)/(3g) = 2rより
gr + v_B² = 6gr
v_B = √(5gr)
 
v_D = √{(v_B² - 2gr) / 3}
= √{(5gr - 2gr) / 3}
v_D = √(gr) … 水平負方向
 
 
 
(8)最終接地点の角度がθ_Dの時のA地点の高さh₀ 
(θ_D = 180ﾟ)
 
v_A = 0として
v_B = √(5gr)となる高さhを求めると
 
力学的エネルギー保存則より
mgh₀ = (1/2)mv_B² 
mgh₀ = (5/2)mgr
h₀ = (5/2)r
(高さh₀は半径rの2.5倍)
 
 
 
(別解)
D地点では遠心力mv²/rと重力mgが釣合っている
mv_D²/r = mg
v_D = √(gr) … D地点の速度の大きさ
 
力学的エネルギー保存則より
mgh₀ = (1/2)mv_D² + 2mgr
mgh₀ = (1/2)mgr + 2mgr
h₀ = (1/2)r + 2r = (5/2)r
 
 
 
(9)最終接地点の角度がθ_Dの時の着地点の位置x_F 
(θ_D = 180ﾟ)
v_D = √(gr) … 水平負方向
 
D地点から着地点Fまでの時間tは
2r = (1/2)gt² 
t² = 4r/g
t = 2√(r/g)
 
x_F = -v_Dt₂ = √(gr)･2√(r/g)
x_F = -2r
 
 
 
(10) V_Bをhで表す
力学的エネルギー保存則より
(1/2)mv_B² = mgh
v_B = √(2gh)