極座標 (1回目)
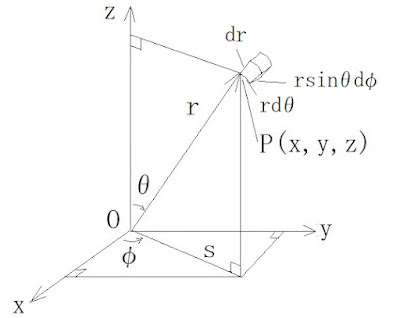
図1. P(x,y,z)の極座標表示と微小体積
▼ P(x,y,z)の極座標表示の導出
図1より
z = rcosθ , s = rsinθ = √(x2+y2)
x = scosφ , y = ssinφ
より
x = rsinθcosφ
y = rsinθsinφ
z = rcosθ
r = √(x2+y2+z2)
θ= Tan-1{√(x2+y2)/z}
φ= Tan-1(y/x)
▼ ヤコビアンの導出
微小体積dV = dxdydz = dr・rdθ・rsinθdφ
= r2sinθdrdθdφ
より
r2sinθ … (ヤコビアン)
▼ 微分公式
u = tant = sint/cost
(d/dt)(1/cost) = sint/cos2t
du/dt = sin2t/cos2t + cost/cost
= tan2t + 1
t = Tan-1u
dt/du = 1 / {tan2t + 1} = 1/(u2+1)
▼ ナブラ∇の導出
∇ = (∂/∂x, ∂/∂y, ∂/∂z)
∂/∂x
= (∂r /∂x)(∂/∂r )
+ (∂θ/∂x)(∂/∂θ)
+ (∂φ/∂x)(∂/∂φ)
r = √(x2+y2+z2)
より
∂r/∂x = 2x(1/2)/√(x2+y2+z2) = x/r
なので
∂r/∂x = x/r = sinθcosφ
∂r/∂y = y/r = sinθsinφ
∂r/∂z = z/r = cosθ
θ= Tan-1{√(x2+y2)/z}
より
∂θ/∂x = (1/z)2x(1/2)/√(x2+y2) /{(x2+y2)/z2+1}
= x/{z√(x2+y2)(x2+y2+z2)/z2} = zx/{r2√(x2+y2)}
= rcosθrsinθcosφ/(r3sinθ) = cosθcosφ/r
なので
∂θ/∂x = cosθcosφ/r
∂θ/∂y = cosθsinφ/r
また
∂θ/∂z = -√(x2+y2)/z2 /{(x2+y2)/z2+1}
= -√(x2+y2)/{z2(x2+y2+z2)/z2}
= -rsinθ/r2 = -sinθ/r
なので
∂θ/∂z = -sinθ/r
φ= Tan-1(y/x)
より
∂φ/∂x = -y/x2 /{(y2/x2) + 1}
= -y/{x2(x2+y2)/x2)} = -y/(x2+y2)
= -rsinθsinφ/(r2sin2θ)
= -sinφ/(rsinθ)
∂φ/∂y = 1/x /{(y2/x2) + 1}
= 1/{x(x2+y2)/x2)} = x/(x2+y2)
= rsinθcosφ/(r2sin2θ)
= cosφ/(rsinθ)
∂φ/∂z = 0
以上をまとめると
∇ =
|∂/∂x|
|∂/∂y|
|∂/∂z|
=
|∂r/∂x ∂θ/∂x ∂φ/∂x||∂/∂r |
|∂r/∂y ∂θ/∂y ∂φ/∂y||∂/∂θ|
|∂r/∂z ∂θ/∂z ∂φ/∂z||∂/∂φ|
=
|sinθcosφ cosθcosφ/r -sinφ/(rsinθ)||∂/∂r |
|sinθsinφ cosθsinφ/r cosφ/(rsinθ)||∂/∂θ|
|cosθ -sinθ/r 0 ||∂/∂φ|
x = rsinθcosφ
y = rsinθsinφ
z = rcosθ
r = √(x2+y2+z2)
θ= Tan-1{√(x2+y2)/z}
φ= Tan-1(y/x)
■ 結果
▼ 極座標表記
x = rsinθcosφ
y = rsinθsinφ
z = rcosθ
r = √(x2+y2+z2)
θ= Tan-1{√(x2+y2)/z}
φ= Tan-1(y/x)
▼ ヤコビアン(Jacobian)
微小体積
dV = dxdydz = r2sinθdrdθdφ
r2sinθ … (ヤコビアン)
▼ ナブラ(Nabla)∇
∇ =
|∂/∂x|
|∂/∂y|
|∂/∂z|
=
|∂r/∂x ∂θ/∂x ∂φ/∂x||∂/∂r |
|∂r/∂y ∂θ/∂y ∂φ/∂y||∂/∂θ|
|∂r/∂z ∂θ/∂z ∂φ/∂z||∂/∂φ|
=
|sinθcosφ cosθcosφ/r -sinφ/(rsinθ)||∂/∂r |
|sinθsinφ cosθsinφ/r cosφ/(rsinθ)||∂/∂θ|
|cosθ -sinθ/r 0 ||∂/∂φ|
▼ P(x,y,z)の極座標表示の導出
図1より
z = rcosθ , s = rsinθ = √(x2+y2)
x = scosφ , y = ssinφ
より
x = rsinθcosφ
y = rsinθsinφ
z = rcosθ
r = √(x2+y2+z2)
θ= Tan-1{√(x2+y2)/z}
φ= Tan-1(y/x)
▼ ヤコビアンの導出
微小体積dV = dxdydz = dr・rdθ・rsinθdφ
= r2sinθdrdθdφ
より
r2sinθ … (ヤコビアン)
▼ 微分公式
u = tant = sint/cost
(d/dt)(1/cost) = sint/cos2t
du/dt = sin2t/cos2t + cost/cost
= tan2t + 1
t = Tan-1u
dt/du = 1 / {tan2t + 1} = 1/(u2+1)
▼ ナブラ∇の導出
∇ = (∂/∂x, ∂/∂y, ∂/∂z)
∂/∂x
= (∂r /∂x)(∂/∂r )
+ (∂θ/∂x)(∂/∂θ)
+ (∂φ/∂x)(∂/∂φ)
r = √(x2+y2+z2)
より
∂r/∂x = 2x(1/2)/√(x2+y2+z2) = x/r
なので
∂r/∂x = x/r = sinθcosφ
∂r/∂y = y/r = sinθsinφ
∂r/∂z = z/r = cosθ
θ= Tan-1{√(x2+y2)/z}
より
∂θ/∂x = (1/z)2x(1/2)/√(x2+y2) /{(x2+y2)/z2+1}
= x/{z√(x2+y2)(x2+y2+z2)/z2} = zx/{r2√(x2+y2)}
= rcosθrsinθcosφ/(r3sinθ) = cosθcosφ/r
なので
∂θ/∂x = cosθcosφ/r
∂θ/∂y = cosθsinφ/r
また
∂θ/∂z = -√(x2+y2)/z2 /{(x2+y2)/z2+1}
= -√(x2+y2)/{z2(x2+y2+z2)/z2}
= -rsinθ/r2 = -sinθ/r
なので
∂θ/∂z = -sinθ/r
φ= Tan-1(y/x)
より
∂φ/∂x = -y/x2 /{(y2/x2) + 1}
= -y/{x2(x2+y2)/x2)} = -y/(x2+y2)
= -rsinθsinφ/(r2sin2θ)
= -sinφ/(rsinθ)
∂φ/∂y = 1/x /{(y2/x2) + 1}
= 1/{x(x2+y2)/x2)} = x/(x2+y2)
= rsinθcosφ/(r2sin2θ)
= cosφ/(rsinθ)
∂φ/∂z = 0
以上をまとめると
∇ =
|∂/∂x|
|∂/∂y|
|∂/∂z|
=
|∂r/∂x ∂θ/∂x ∂φ/∂x||∂/∂r |
|∂r/∂y ∂θ/∂y ∂φ/∂y||∂/∂θ|
|∂r/∂z ∂θ/∂z ∂φ/∂z||∂/∂φ|
=
|sinθcosφ cosθcosφ/r -sinφ/(rsinθ)||∂/∂r |
|sinθsinφ cosθsinφ/r cosφ/(rsinθ)||∂/∂θ|
|cosθ -sinθ/r 0 ||∂/∂φ|
x = rsinθcosφ
y = rsinθsinφ
z = rcosθ
r = √(x2+y2+z2)
θ= Tan-1{√(x2+y2)/z}
φ= Tan-1(y/x)
■ 結果
▼ 極座標表記
x = rsinθcosφ
y = rsinθsinφ
z = rcosθ
r = √(x2+y2+z2)
θ= Tan-1{√(x2+y2)/z}
φ= Tan-1(y/x)
▼ ヤコビアン(Jacobian)
微小体積
dV = dxdydz = r2sinθdrdθdφ
r2sinθ … (ヤコビアン)
▼ ナブラ(Nabla)∇
∇ =
|∂/∂x|
|∂/∂y|
|∂/∂z|
=
|∂r/∂x ∂θ/∂x ∂φ/∂x||∂/∂r |
|∂r/∂y ∂θ/∂y ∂φ/∂y||∂/∂θ|
|∂r/∂z ∂θ/∂z ∂φ/∂z||∂/∂φ|
=
|sinθcosφ cosθcosφ/r -sinφ/(rsinθ)||∂/∂r |
|sinθsinφ cosθsinφ/r cosφ/(rsinθ)||∂/∂θ|
|cosθ -sinθ/r 0 ||∂/∂φ|