衝突 (1回目)

2023/11/1(水)
衝突 (1回目)
 
(collision)
 
球同士の衝突
 
■ 導出
▼ 定義
大文字(太字)はベクトル
右下添字は球番号
 
P:球の位置ベクトル
V:球の速度
A:球の加速度
t:経過時間
r:球の半径
E:球の移動方向の単位ベクトル
R:球の軌跡
s:距離
':衝突後
 
▼ 衝突

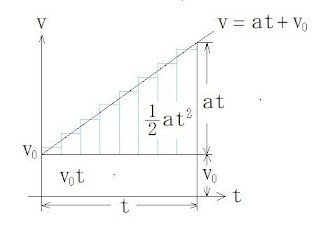
図1.加速度と位置の関係

 
ΔV = AΔt
ΔP = VΔt + (1/2)AΔt² 
v = |ΔP|  … 速さ
 

 
 

図2. d = √[r² - {|P|² - (P･E)²}]
s₁ = -P･E - d, s₂ = -P･E + d
 
r = r₁ + r₂  … 半径rの球
P = P₁ - P₂  … 球2が原点の時の球1の位置
 
|R| = r    … 球
に
R = P + sE  … 球1の軌跡
を代入
|P + sE| = r
(P + sE)(P + sE) = r² 
P･P + 2s(P･E) + s²(E･E) = r² 
s² +  2s(P･E) + P･P - r² = 0
 
d = (P･E)² - P･P + r²  … 判別式
s = -P･E±√(d)       … 2球間距離
 
s₁ = -P･E - √(d)  … 手前
s₂ = -P･E + √(d)  … 奥
 
(d ＜ 0)の時、衝突なし
(d ≧ 0)の時
　(s₂ ＜ 0 または v ＜ s₁)の時、衝突なし  
　その他、衝突
 
 
▼ 衝突(|Δt| << 1のとき)
dV = Adt
dP = Vdt
 
r = r₁ + r₂  … 半径rの球
P = P₁ - P₂  … 球2が原点の時の球1の位置
 
P･P = ≦ r²  … (|P| ≦ r)
の時、衝突
 
 
■ 結果
▼ 定義
大文字(太字)はベクトル
右下添字は球番号
 
P:球の位置ベクトル
m:球の質量
V:球の速度
A:球の加速度
t:経過時間
r:球の半径
E:球の移動方向の単位ベクトル
R:球の軌跡
s:距離(右下添字は手前と奥)
':衝突後
 
 
▼ 衝突
ΔV = AΔt
ΔP = VΔt + (1/2)AΔt² 
v = |ΔP|  … 速さ
 
r = r₁ + r₂  … 半径rの球
P = P₁ - P₂  … 球2が原点の時の球1の位置
 
|R| = r    … 球
R = P + Es  … 球1の軌跡
 
d = (P･E)² - P･P + r²  … 判別式
s = -P･E±√(d)       … 2球間距離
 
s₁ = -P･E - √(d)  … 手前
s₂ = -P･E + √(d)  … 奥
 
(d ＜ 0)の時、衝突なし
(d ≧ 0)の時
　(s₂ ＜ 0 または v ＜ s₁)の時、衝突なし  
　その他、衝突
 
 
▼ 衝突(|Δt| << 1のとき)
dV = Adt
dP = Vdt
 
r = r₁ + r₂  … 半径rの球
P = P₁ - P₂  … 球2が原点の時の球1の位置
 
P･P = ≦ r²  … (|P| ≦ r)
の時、衝突