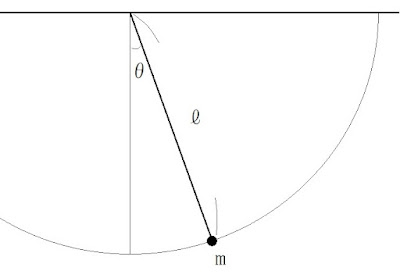
振り子 (1回目)

2023/12/20(水)
振り子 (1回目)
 
振り子(Pendulum)
微分方程式
 
■ 図

図1.

 
■ 導出
▼ 定義
ℓ :紐の長さ(m)
m :質点の質量(kg)
θ:鉛直下方向からの角度(rad)
g :重力加速度
 
▼ 位置r
x:支点からの右方向の変位(m)
y:支点からの下方向の変位(m)
r = (x, y) = (ℓsinθ, ℓcosθ)
 
▼ 速度v
v = r(・) = (x(・), y(・)) = (ℓθ(・)cosθ, -ℓθ(・)sinθ)
 
▼ 運動エネルギーT
T = (1/2)mv² = (1/2)mℓ²θ(・)²{cos²θ + (-sinθ)²}
= (1/2)mℓ²θ(・)² 
 
▼ 位置エネルギーV
支点を0として
V = mg(-y) = -mgℓcosθ
 
▼ ラグランジアンL
L = T - V
= (1/2)mℓ²θ(・)² + mgℓcosθ
 
▼ ラグランジュ方程式
q_i = θとして
(d/dt)(∂L/∂q(・)_i) = (∂L/∂q_i)
を解く
 
(d/dt)(∂/∂θ(・)){(1/2)mℓ²θ(・)² + mgℓcosθ}
= (d/dt)(mℓ²θ(・)) = mℓ²θ(･･
)(∂/∂θ){(1/2)mℓ²θ(・)² + mgℓcosθ}
= -mgℓsinθ
より
 
mℓ²θ(･･) = -mgℓsinθ
θ(･･) = -(g/ℓ)sinθ
 
 
■ ニュートンの運動方程式(別解1)
▼ ニュートンの運動方程式
F= ma より
極座標表記で動径方向は一定なので
θ方向のみ考える
 
F = -mgsinθ
ma = mℓθ(･･
)より
 
mℓθ(･･) = -mgsinθ
θ(･･) = -(g/ℓ)sinθ
 
 
■ ニュートンの運動方程式(別解2)
▼ 加速度a
r = (x, y) = ℓ(sinθ, cosθ)
a = v(・) = ℓ(d/dt)(θ(・)cosθ, -θ(・)sinθ)
= ℓ(θ(･･)cosθ - θ(・)²sinθ, -θ(･･)sinθ - θ(・)²cosθ)
 
▼ ニュートンの運動方程式
F = ma より
F = (0, mg)
ma = mℓ(θ(･･)cosθ - θ(・)²sinθ, -θ(･･)sinθ - θ(・)²cosθ)
 
x座標
mℓ(θ(･･)cosθ - θ(・)²sinθ) = 0
θ(･･)cosθ = θ(・)²sinθ
 
θ(・)² = θ(･･)cosθ/sinθ
 
をy座標に代入
mℓ(-θ(･･)sinθ - θ(・)²cosθ) = mg
-θ(･･)sinθ - θ(・)²cosθ = g/ℓ
-θ(･･)sinθ - (θ(･･)cosθ/sinθ)cosθ = g/ℓ
θ(･･)sin²θ + θ(･･)cos²θ = -(g/ℓ)sinθ
θ(･･) = -(g/ℓ)sinθ
 
 
■ 正準方程式(別解3)
▼ ラグランジアンL
L = T – V
= (1/2)mℓ²θ(・)² + mgℓcosθ
 
▼ 一般運動量
p_i = (∂L/∂q(・)_i) = (∂L/∂θ(・)_i)
より
p = (∂/∂θ(・)){(1/2)mℓ²θ(・)² + mgℓcosθ}
= mℓ²θ(・) 
 
▼ 角速度の一般運動量表記
θ(・) = p/(mℓ²)
 
▼ ラグランジアンLの一般運動量表記
L = T – V
= (1/2)mℓ²θ(・)² + mgℓcosθ
= (1/2)mℓ²{p/(mℓ²)}² + mgℓcosθ
= (1/2)p²/(mℓ²) + mgℓcosθ
 
▼ ハミルトニアンH
H(q_α, p_α, t) = p_iq(・)_i - L(q_α, q(・)_α, t)
= p_iθ(・)_i - L(q_α, p_α, t)
= pθ(・) - L(θ, p, t)
= p²/(mℓ²) - {(1/2)p²/(mℓ²) + mgℓcosθ}
= {p² - (1/2)p²}/(mℓ²) - mgℓcosθ
= (1/2)p²/(mℓ²) - mgℓcosθ
 
H = (1/2)p²/(mℓ²) - mgℓcosθ
 
▼ ハミルトニアンH(別解)
θ(・) = p/(mℓ²)
T = (1/2)mℓ²θ(・)² = (1/2)mℓ²p²/(mℓ²)² 
= (1/2)p²/(mℓ²)
V = -mgℓcosθ
H = T + V = (1/2)p²/(mℓ²) - mgℓcosθ
 
▼ 正準運動方程式
H = (1/2)p²/(mℓ²) - mgℓcosθ
 
q_i = θ_iとして
∂H/∂q_i = -p(・)_i 
∂H/∂p_i =  q(・)_i 
∂H/∂t  = -∂L/∂t
を解く
 
p(・) = -∂H/∂θ
= -(∂/∂θ){(1/2)p²/(mℓ²) - mgℓcosθ}
= -mgℓsinθ
 
θ(・) = ∂H/∂p
= (∂/∂p){(1/2)p²/(mℓ²) - mgℓcosθ}
= p/(mℓ²)
 
∂H/∂t = (∂/∂t){(1/2)p²/(mℓ²) - mgℓcosθ}
= pp(・)/(mℓ²) + mgℓθ(・)sinθ
 
∂L/∂t = -(∂/∂t){(1/2)p²/(mℓ²) + mgℓcosθ}
= -pp(・)/(mℓ²) + mgℓθ(・)sinθ
より
2pp(・)/(mℓ²) = 0
pp(・) = 0
 
 
まとめると
p(・) = -mgℓsinθ
θ(・) = p/(mℓ²)より
p = mℓ²θ(・) の両辺tで微して
p(・) = mℓ²θ(･･
)よって
p(・) = mℓ²θ(･･) = -mgℓsinθ
θ(･･) = -(g/ℓ)sinθ
 
 
■ 結果
▼ 定義
ℓ :紐の長さ(m)
m :質点の質量(kg)
θ:鉛直下方向からの角度(rad)
g :重力加速度
 
▼ 微分方程式
θ(･･) = -(g/ℓ)sinθ