サイコロの出目の和 (3回目)

2024/2/18(日)
サイコロの出目の和 (3回目)
 
出目1～dのサイコロn個の和がkとなる場合の集合
 
■ 場合の集合
▼ 集合の定義
集合Aの場合の数(要素数)は|A|と書く
 
n個のサイコロの出目1～dの和がkとなる集合をAとする
(|A|を求めることが目的)
 
n個のサイコロの出目1～?の和がkとなる集合をA₀とする
(出目がd以下とdを超える場合のすべてを含む)
 
i番目のサイコロの出目がdを超える集合をA_iとする
(i=1～n, i番目以外がdを超える場合も含む)
 
 
▼ 集合の式
(A₁∪A₂∪…∪A_n)は少なくとも1個の出目はdを超え
Aは出目がd以下のみの場合なので
A ∩ (A₁∪A₂∪…∪A_n) = ∅
 
また
A₀ = A ∪ (A₁∪A₂∪…∪A_n)
なので
 
|A| = |A₀| - |A₁∪A₂∪…∪A_n|
となる
 
 
▼ |A₁∪A₂∪…∪A_n|(n = 3の時)を考える
例

 

 
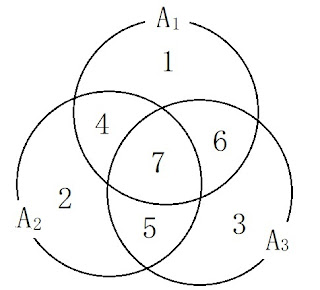
|A₁∪A₂∪A₃|
= |A₁|+|A₂|+|A₃|
- |A₁∩A₂|-|A₁∩A₃|-|A₂∩A₃|
+ |A₁∩A₂∩A₃|
 
= (1+4+6+7) + (2+4+5+7) + (3+5+6+7)
- (4+7) - (5+7) – (6+7)
+ (7)
 
= (1+6) + (2+4) + (3+5) + (7)
= 1 + 2 + 3 + 4 + 5 + 6 + 7
 
つまり
|A₁|+|A₂|+|A₃|には
|A₁∩A₂∩A₃|を除く|A₁∩A₂|,|A₁∩A₃|,|A₂∩A₃|
の部分が2回ずつと
|A₁∩A₂∩A₃|の部分が3回ずつ含まれる
|A₁∩A₂|,|A₁∩A₃|,|A₂∩A₃|を引くと
2回分が1回分だけになるが
|A₁∩A₂∩A₃|の部分を3回分引くことになるので
|A₁∩A₂∩A₃|を1回分足している
 
 
▼ |A₁∪A₂∪…∪A_n|(n = 4の時)を考える
例

 

 
 
|A₁∪A₂∪A₃∪A₄|
= |A₁|+|A₂|+|A₃|+|A₄|
- |A₁∩A₂|-|A₁∩A₃|-|A₁∩A₄|-|A₂∩A₃|-|A₂∩A₄|-|A₃∩A₄|
+ |A₁∩A₂∩A₃|+|A₁∩A₂∩A₄|+|A₁∩A₃∩A₄|+|A₂∩A₃∩A₄|
- |A₁∩A₂∩A₃∩A₄|
 
= (1+5+8+9+11+12+13) + (2+5+6+9+10+12+13)
+ (3+6+7+9+10+11+13) + (4+7+8+10+11+12+13)
- (5+9+12+13) - (9+11+13) - (8+11+12+13)
- (6+9+10+13) - (10+12+13) - (7+10+11+13)
+ (9+13) + (12+13) + (11+13) + (10+13)
- (13)
 
= (1+8+11) + (2+5+12) + (3+6+9) + (4+7+10)
- (9+11+13) - (10+12+13)
+ (9+13) + (12+13) + (11+13) + (10+13)
- (13)
 
= (1+8+11) + (2+5+12) + (3+6+9) + (4+7+10)
+ (13)
 
= 1+2+3+4+5+6+7+8+9+10+11+12+13
 
 
▼ |A₁∪A₂∪…∪A_n|を考える
|A₁∪A₂∪…∪A_n|
= (|A₁|+|A₂|+…+|A_n|)
- (|A₁∩A₂|+…+|A₁∩A_n|+…+|A₂∩A₃|+…+|A_n-1∩A_n|)
+(-1)^r-1(|A₁∩A₂∩…∩A_r|+…+|A_n-r+1∩A_n-r+2∩…∩A_n|)
+(-1)^n-1|A₁∩A₂∩…∩A_n|
 
 
▼ |A|の集合の式
|A| = |A₀| - |A₁∪A₂∪…∪A_n|
= |A₀|
- (|A₁|+|A₂|+…+|A_n|)
+ (|A₁∩A₂|+…+|A₁∩A_n|+…+|A₂∩A₃|+…+|A_n-1∩A_n|)
+(-1)^r(|A₁∩A₂∩…∩A_r|+…+|A_n-r+1∩A_n-r+2∩…∩A_n|)
+(-1)ⁿ|A₁∩A₂∩…∩A_n|
となる
 
■ 結果
▼ 集合の定義
集合Aの場合の数(要素数)は|A|と書く
 
n個のサイコロの出目1～dの和がkとなる集合をAとする
(|A|を求めることが目的)
 
n個のサイコロの出目1～?の和がkとなる集合をA₀とする
(出目がd以下とdを超える場合のすべてを含む)
 
i番目のサイコロの出目がdを超える集合をA_iとする
(i=1～n, i番目以外がdを超える場合も含む)
 
▼ 集合
出目1～dのサイコロn個の和がkとなる場合の集合
|A| = |A₀| - |A₁∪A₂∪…∪A_n|
= |A₀|
- (|A₁|+|A₂|+…+|A_n|)
+ (|A₁∩A₂|+…+|A₁∩A_n|+…+|A₂∩A₃|+…+|A_n-1∩A_n|)
+(-1)^r(|A₁∩A₂∩…∩A_r|+…+|A_n-r+1∩A_n-r+2∩…∩A_n|)
+(-1)ⁿ|A₁∩A₂∩…∩A_n|