特殊相対性理論 (1回目)

2024/11/12(火)
特殊相対性理論 (1回目)
 
(special relativity)
 
1. 光速度一定から動いているものの時間を求める

 
光速度c
静止しているAさんの時間t
速度vで移動しているBさんの時間t'
 
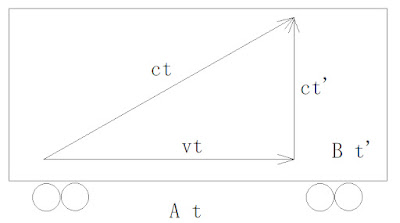
Aさんから見たBさんの移動距離x = vt
Bさんから見たBさんの移動距離x'= v't' = 0
Bさんが見た光の移動距離ct'
Aさんが見た光の移動距離ct
 
γ = 1/√(1 - v²/c²)   … ローレンツ係数

 
(ct')² = (ct)² - (vt)² より
t' = t√(1 - v²/c²) = t/γ … t:静止座標系, t':慣性座標系
 
 
2. 不変量(固有時間τと固有長s)
不変量τ² (固有時間τ)とdτ² の定義(x'= v't' = 0より以下が成り立つ)
τ² = (ct')² - (v't')² = (ct)² - (vt)² = (ct')² - x'² = (ct)² - x² 
dτ² = (cdt)² - dx² - dy² - dz²  … ①(固有時間dτ)
ds² = -(cdt)² + dx² + dy² + dz² = -dτ²   … (固有長ds)
 
 
3. 四元速度
x = (x₀, x₁, x₂, x₃) = (ct, x, y, z) … 四元位置
u = (u₀, u₁, u₂, u₃) = (cdt/dτ, dx/dτ, dy/dτ, dz/dτ) … 四元速度
①式を(cdt)² で割ると
dτ²/(cdt)² = 1 - (1/c²){(dx/dt)² + (dy/dt)² + (dz/dt)²}
= 1 - v²/c² = (1/γ)² 
dτ/(cdt) = 1/γ 
u₀ = cdt/dτ = γ , u₁ = dx/dτ = (cdt/dτ){dx/(cdt)} = γ(v_x/c)
u = (u₀, u₁, u₂, u₃) = (γ, γ(v_x/c), γ(v_y/c), γ(v_z/c)) … 四元速度
 
 
4. 四元運動量
q = (q₀, q₁, q₂, q₃) = mcu = mc(u₀, u₁, u₂, u₃) … 四元運動量
= (γmc, γmv_x, γmv_y, γmv_z)
p = (p_x, p_y, p_z) = (γmv_x, γmv_y, γmv_z) … 運動量
q = (q₀, q₁, q₂, q₃) = (γmc, p_x, p_y, p_z)
 
①式をdτ² で割ると
1 = (cdt/dτ)² - (dx/dτ)² - (dy/dτ)² - (dz/dτ)² =  u₀² - u₁² - u₂² - u₃² 
(mc)² 倍して
(mc)² = (mc)²(u₀² - u₁² - u₂² - u₃²) = q₀² - p_x² - p_y² - p_z² = q₀² - |p|² 
(mc)² = q₀² - |p|²  … ②
 
 
5. マクローリン展開
f⁽⁰⁾(x) = ax² + bx + c , f⁽⁰⁾(0) = c
f⁽¹⁾(x) = 2ax + 1b , f⁽¹⁾(0) = 1b
f⁽²⁾(x) = 1･2a , f⁽²⁾(0) = 1･2a
f⁽⁰⁾(x) = f⁽⁰⁾(0) + f⁽¹⁾(0)x/1 + f⁽²⁾(0)x²/(2･1) = Σ_n=0^∞ f⁽ⁿ⁾(0)xⁿ/n!
 
f⁽⁰⁾(x) = √(1+x²)  , f⁽⁰⁾(0) = 1
f⁽¹⁾(x) = x(1+x²)^-1/2  , f⁽¹⁾(0) = 0
f⁽²⁾(x) = (1+x²)^-1/2 - x²(1+x²)^-3/2  , f⁽²⁾(0) = 1
√(1+x²) ≒ 1 + x²/2 … |x| << 1
 
 
6. 全エネルギー(|v| << 1)
(mc)² = q₀² - |p|²  … ②式より
q₀/(mc) = √{1 + (|p|/(mc))²}
≒ 1 + (1/2)(|p|/(mc))²  … |v| << 1(マクローリン展開)
q₀c = mc² + |p|²/(2m) … (静止+運動)エネルギー( p²/(2m) = (1/2)mv² )
よって
E = q₀c = mc² + |p|²/(2m)  … 全エネルギー(|v| << 1)

 
 
7. 特殊相対性理論の全エネルギー
(mc)² = q₀² - |p|²  … ②式より
(mc²)² = (q₀c)² - |pc|² = E² - |pc|²  … 不変量(静止エネルギー mc² )
E² = (mc²)² + |pc|²  … 全エネルギー(|v| ≦ cに拡張)