N88-BASICで偶数回目に表が出る確率 (1回目)
2021/11/23(火)
N88-BASICで偶数回目に表が出る確率 (1回目)
コインを表が出るまで投げた回数が
偶数か奇数かを当てるゲームをする
例えば
裏,裏,表(必ず表で終了)と出れば
3回投げたので奇数に賭けた人の勝ちです
裏,裏,裏,表(必ず表で終了)と出れば
4回投げたので偶数に賭けた人の勝ちで
実際にコインを投げて見ると
奇数に掛けた方が良く勝てます
不思議です・・・
が、よく考えてみると
1回目が表の確率は1/2
2回目が表の確率は1/4 (1回目裏は1/2 その内の1/2)
3回目が表の確率は1/8
4回目が表の確率は1/16
5回目が表の確率は1/32
6回目が表の確率は1/64
・・・
N88-BASICで偶数回目に表が出る確率 (1回目)
コインを表が出るまで投げた回数が
偶数か奇数かを当てるゲームをする
例えば
裏,裏,表(必ず表で終了)と出れば
3回投げたので奇数に賭けた人の勝ちです
裏,裏,裏,表(必ず表で終了)と出れば
4回投げたので偶数に賭けた人の勝ちで
実際にコインを投げて見ると
奇数に掛けた方が良く勝てます
不思議です・・・
が、よく考えてみると
1回目が表の確率は1/2
2回目が表の確率は1/4 (1回目裏は1/2 その内の1/2)
3回目が表の確率は1/8
4回目が表の確率は1/16
5回目が表の確率は1/32
6回目が表の確率は1/64
・・・
なので
奇数回で終了する確率は1/2+1/8+1/32+ … と
1/2より大きいくなるので
偶数回で終了する確率は(1/4+1/16+1+64+ … )
1/2より小さくなります
ではどの位有利なのかを計算してみます
偶数回で終了する確率pは、上記の2,4,6,… 回目
の合計になるので、
p = 1/4 + 1/16 + 1/64 + …
n
= lim Σ(1/4)i
n→∞ i=1
を計算すれば良い
n
(r-1)Σ(r)i = rn+1+rn+ … +r2 - (rn+ … +r2+r)
i=1
= rn+1 - r
n
Σ(r)i = ( rn+1 - r ) / (r - 1)
i=1
(等比級数の和)
また、|r| < 1ならlim rn = 0
n→∞
(例0.1×0.1×...は0に近づく)
を使って
n
p = lim Σ(1/4)i
n→∞ i=1
= lim { (1/4)n+1 - (1/4) } / (1/4 - 1)
n→∞
= { 0 - (1/4) } / (1/4 - 4/4)
= (-1/4) / (-3/4)
= (1/4) / (3/4)
= 1/4 × 4/3
= 1/3 … 偶数回
奇数回の確率 = 1 - 1/3 = 2/3
つまり
偶数回で終わる確率1/3
奇数回で終わる確率2/3
という結果になります
どちらがジュースを買いに行くか
コインで決めようとなった場合、
表が出るまでの回数が偶数か奇数
か賭けようと言い、奇数に賭ける
ことが出来れば、確率的には
得できます
それでも、運悪く買いに行くことに
なるかも...
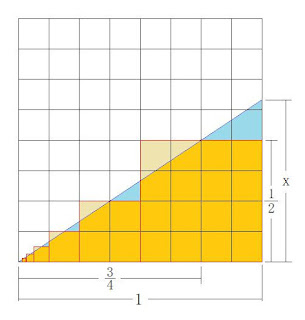
この確率の計算を図で解いてみると
1辺1の長さの面積1の正方形の
1/ 4の面積の正方形 +
1/16の面積の正方形 +
1/64の面積の正方形 + …
は図のオレンジ色+ベージュ色の面積に等しい
これは、底辺1、高さx(オレンジ+水色)の
直角三角形の面積に等しい
x : 1/2 = 1 : 3/4より
x = 1/2 × 4/3 = 2/3
直角三角形の面積は
1×2/3×1/2 = 1/3
よって
n
p = lim Σ(1/4)i
n→∞ i=1
= 1/4 + 1/16 + 1/64 + …
= 1/3
となります
このゲームをシミュレートしてみました
NL-BASICとblg~.zip(coin001.bas)は
このブログからダウンロードできます
奇数回で終了する確率は1/2+1/8+1/32+ … と
1/2より大きいくなるので
偶数回で終了する確率は(1/4+1/16+1+64+ … )
1/2より小さくなります
ではどの位有利なのかを計算してみます
偶数回で終了する確率pは、上記の2,4,6,… 回目
の合計になるので、
p = 1/4 + 1/16 + 1/64 + …
n
= lim Σ(1/4)i
n→∞ i=1
を計算すれば良い
n
(r-1)Σ(r)i = rn+1+rn+ … +r2 - (rn+ … +r2+r)
i=1
= rn+1 - r
n
Σ(r)i = ( rn+1 - r ) / (r - 1)
i=1
(等比級数の和)
また、|r| < 1ならlim rn = 0
n→∞
(例0.1×0.1×...は0に近づく)
を使って
n
p = lim Σ(1/4)i
n→∞ i=1
= lim { (1/4)n+1 - (1/4) } / (1/4 - 1)
n→∞
= { 0 - (1/4) } / (1/4 - 4/4)
= (-1/4) / (-3/4)
= (1/4) / (3/4)
= 1/4 × 4/3
= 1/3 … 偶数回
奇数回の確率 = 1 - 1/3 = 2/3
つまり
偶数回で終わる確率1/3
奇数回で終わる確率2/3
という結果になります
どちらがジュースを買いに行くか
コインで決めようとなった場合、
表が出るまでの回数が偶数か奇数
か賭けようと言い、奇数に賭ける
ことが出来れば、確率的には
得できます
それでも、運悪く買いに行くことに
なるかも...
この確率の計算を図で解いてみると
1辺1の長さの面積1の正方形の
1/ 4の面積の正方形 +
1/16の面積の正方形 +
1/64の面積の正方形 + …
は図のオレンジ色+ベージュ色の面積に等しい
これは、底辺1、高さx(オレンジ+水色)の
直角三角形の面積に等しい
x : 1/2 = 1 : 3/4より
x = 1/2 × 4/3 = 2/3
直角三角形の面積は
1×2/3×1/2 = 1/3
よって
n
p = lim Σ(1/4)i
n→∞ i=1
= 1/4 + 1/16 + 1/64 + …
= 1/3
となります
このゲームをシミュレートしてみました
NL-BASICとblg~.zip(coin001.bas)は
このブログからダウンロードできます