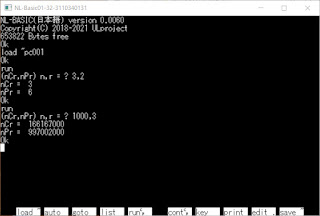
N88-BASICで順列組合せ
2021/11/7(日)
N88-BASICで順列組合せ
順列 nPr(Permutation)と
組合せnCr(Combination)の解説です
順列は、異なるn個からr個選んで並べた
並べ方の数です
nPr 通りの並べ方があります(n≧r)
nPr = n・(n-1)・ … ・(n-r+1)
nから1ずつ減らしてr個掛ける
例
A,B,Cの3人から第1,2走者を選ぶ
1□ 2□
上記、1□にA~Cの3人中1人を座らせ
2□に残り2人中1人を座らせる
3・2 = 6通りの選び方があります
3P2 = 3・2 = 6です
1 2
A-B
A-C
B-C
B-A
C-A
C-B
の6通り(3・2通り)です
n個すべてを並べる場合は
n!(nの階乗factorial)を使います
n! = nPn
n! = n・(n-1)!
1! = 1・0! = 1より0! = 1
また nPr = n!/(n-r)! です
組合せ(Combination)は
異なるn個からr個選ぶ
選び方の数です
nCr 通りの選び方があります(n≧r)です
nPrは選んだr個を並替えますが
nCrは選ぶだけで並替えません
nCr = nPr/r! = n・(n-1)・ … ・(n-r+1)/r!
nから1ずつ減らしてr個掛けてr!で割る
例
A,B,Cの3人から2人選んで並べると
3P2 = 3・2 = 6通りです
1 2
A-B
A-C
B-C
B-A
C-A
C-B
しかし、
A-BとB-Aは同じAとBの組合せです
2個を並替えた場合の数(2!=2)ずつ同じ組合せが
存在するので2!で割ります
3C2 = 3P2/2! = 3・2/2 = 6/2 = 3通り
1 2
A-B (B-Aは同じ組合せ)
A-C (C-Aは同じ組合せ)
B-C (C-Bは同じ組合せ)
の3通りです
nPr = nCr ・ r!
nCr = nPr / r!
です
また
nCr = nPr/r! = n!/{(n-r)!r!}
や
nCn-r = n!/[{n-(n-r)}!(n-r)!]
= n!/{r!(n-r)!} = nCr
も便利な法則です
ちなみに
nC0 = nCn = n!/(0!・n!) = 1
0C0 = 0!/(0!・0!) = 1
です
nCrは二項式(項が2個の式)のn乗
(a+b)nを展開した各項の係数を表して
いてパスカルの三角形の数値と同じです
____1
___1_1
__1_2_1
_1_3_3_1
1_4_6_4_1
(各数字が左上+右上になっている)
なのでnCrが出てくる法則で二項~と
言う名称を良く目にします
プログラムでは整数型の扱える数が小さいので
倍精度実数型で計算しています
倍精度の有効桁数を超えると誤差が出ます
組合せの計算は、出来るだけオーバーフロー
しないよう以下の工夫をしています
実数型を使用して
nCr
= nPr/r!
= {(n-r+1)/1}{(n-r+2)/2}…{(n-r+r)/r}
で計算し、割り切れないとき誤差が出ますが
最終結果が整数になることを利用して
最終結果の小数を四捨五入して誤差を
修正しています
NL-BASICとblg~.zip(pc001.bas)は
このブログ(以下のリンク)から
ダウンロードできます
順列 nPr(Permutation)と
組合せnCr(Combination)の解説です
並べ方の数です
nPr 通りの並べ方があります(n≧r)
nから1ずつ減らしてr個掛ける
例
A,B,Cの3人から第1,2走者を選ぶ
1□ 2□
上記、1□にA~Cの3人中1人を座らせ
2□に残り2人中1人を座らせる
3・2 = 6通りの選び方があります
3P2 = 3・2 = 6です
1 2
A-B
A-C
B-C
B-A
C-A
C-B
の6通り(3・2通り)です
n個すべてを並べる場合は
n!(nの階乗factorial)を使います
n! = nPn
n! = n・(n-1)!
1! = 1・0! = 1より0! = 1
また nPr = n!/(n-r)! です
組合せ(Combination)は
異なるn個からr個選ぶ
選び方の数です
nCr 通りの選び方があります(n≧r)です
nCrは選ぶだけで並替えません
nから1ずつ減らしてr個掛けてr!で割る
例
A,B,Cの3人から2人選んで並べると
3P2 = 3・2 = 6通りです
1 2
A-B
A-C
B-C
B-A
C-A
C-B
しかし、
A-BとB-Aは同じAとBの組合せです
2個を並替えた場合の数(2!=2)ずつ同じ組合せが
存在するので2!で割ります
3C2 = 3P2/2! = 3・2/2 = 6/2 = 3通り
1 2
A-B (B-Aは同じ組合せ)
A-C (C-Aは同じ組合せ)
B-C (C-Bは同じ組合せ)
の3通りです
nPr = nCr ・ r!
nCr = nPr / r!
です
また
nCr = nPr/r! = n!/{(n-r)!r!}
や
nCn-r = n!/[{n-(n-r)}!(n-r)!]
= n!/{r!(n-r)!} = nCr
も便利な法則です
ちなみに
nC0 = nCn = n!/(0!・n!) = 1
0C0 = 0!/(0!・0!) = 1
です
nCrは二項式(項が2個の式)のn乗
(a+b)nを展開した各項の係数を表して
いてパスカルの三角形の数値と同じです
____1
___1_1
__1_2_1
_1_3_3_1
1_4_6_4_1
(各数字が左上+右上になっている)
なのでnCrが出てくる法則で二項~と
言う名称を良く目にします
プログラムでは整数型の扱える数が小さいので
倍精度実数型で計算しています
倍精度の有効桁数を超えると誤差が出ます
組合せの計算は、出来るだけオーバーフロー
しないよう以下の工夫をしています
実数型を使用して
nCr
= nPr/r!
= {(n-r+1)/1}{(n-r+2)/2}…{(n-r+r)/r}
で計算し、割り切れないとき誤差が出ますが
最終結果が整数になることを利用して
最終結果の小数を四捨五入して誤差を
修正しています
NL-BASICとblg~.zip(pc001.bas)は
このブログ(以下のリンク)から
ダウンロードできます