N88-BASICでモンティホール問題 (2回目)

2021/12/12(日)
N88-BASICでモンティホール問題 (2回目)

(Monty Hall problem)

それぞれ〇,×,×が入った3箱がある
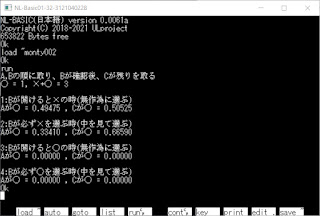
Aが1箱選びBが残りから1箱選び残りはCが貰う
次の場合であった時、A,Cが〇を貰える確率は？
(1) Bが開けると×の時(無作為に選ぶ), A=1/2, C=1/2
(2) Bが必ず×を選ぶ時(中を見て選ぶ), A=1/3, C=2/3
(3) Bが開けると〇の時(無作為に選ぶ), A=0/2, C=0/2
(4) Bが必ず〇を選ぶ時(中を見て選ぶ), A=0/3, C=0/3
 
(注)分母は全体を3として条件付き確率の分母を表した
 
解説
以下、分かりやすいように×,×をＸ,ｘで表す事にする

(1) Bが開けると×の時					(2) Bが必ず×を選ぶ時
A	B	A結果	C結果		A	B	A結果	C結果
〇1/3	Ｘ1/6	〇1/6	ｘ1/6		〇1/3	Ｘ1/6	〇1/6	ｘ1/6
	ｘ1/6	〇1/6	Ｘ1/6			ｘ1/6	〇1/6	Ｘ1/6
Ｘ1/3	〇1/6	Ｘ0	ｘ0		Ｘ1/3	ｘ1/6	Ｘ1/6	〇1/6
	ｘ1/6	Ｘ1/6	〇1/6			ｘ1/6	Ｘ1/6	〇1/6
ｘ1/3	〇1/6	ｘ0	Ｘ0		ｘ1/3	Ｘ1/6	ｘ1/6	〇1/6
	Ｘ1/6	ｘ1/6	〇1/6			Ｘ1/6	ｘ1/6	〇1/6

A〇(2/6) / 全体(4/6)=1/2　　　　　　　　　A〇(2/6) / 全体(6/6)= 1/3

C〇(2/6) / 全体(4/6)=1/2　　　　　　　　　C〇(4/6) / 全体(6/6)= 2/3

  

(3) Bが開けると〇の時					(4) Bが必ず〇を選ぶ時
A	B	A結果	C結果		A	B	A結果	C結果
〇1/3	Ｘ1/6	〇0	ｘ0		〇1/3	Ｘ1/6	〇0	ｘ0
	ｘ1/6	〇0	Ｘ0			ｘ1/6	〇0	Ｘ0
Ｘ1/3	〇1/6	Ｘ1/6	ｘ1/6		Ｘ1/3	〇1/6	Ｘ1/6	ｘ1/6
	ｘ1/6	Ｘ0	〇0			〇1/6	Ｘ1/6	ｘ1/6
ｘ1/3	〇1/6	ｘ1/6	Ｘ1/6		ｘ1/3	〇1/6	ｘ1/6	Ｘ1/6
	Ｘ1/6	ｘ0	〇0			〇1/6	ｘ1/6	Ｘ1/6

A〇(0/6) / 全体(2/6)=0/1　　　　　　　　　A〇(0/6) / 全体(4/6)=0/2
C〇(0/6) / 全体(2/6)=0/1　　　　　　　　　C〇(0/6) / 全体(4/6)=0/2
 
 
モンティホール問題は
3箱の内、1箱だけ当たりが入っている
1箱選んだ後、残りの2箱の内、外れ1箱が開けられる
このとき、開いていない残りの箱と交換してもらえる
交換する方が得か、交換しない方が得か
という問題です
 
上記(2)のAが交換しない、Cが交換する場合
なので交換する方が得です
 
NL-BASICとblg～.zip(monty002.bas)は
このブログ(以下のリンク)から
ダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい