N88-BASICでモンティホール問題 (3回目) (トランプ問題)
2021/12/14(火)
N88-BASICでモンティホール問題 (3回目)
(Monty Hall problem)
モンティーホール問題と似た問題
トランプの問題
52枚のトランプからAが1枚取る
この時Aが1のカードを取っている
確率は4/52 = 1/13
次にBが残りから1枚取って
カードを見ると1以外だった。
Aのカードが1である確率は変わったか
という問題です
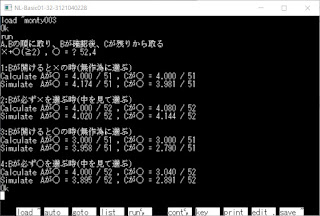
下記(1)のr=4,s=48,n=52の
Aの場合なので
r/(n-1) = 4/(52-1) = 4/51
なので確率は増加
Bが残りのカードから1以外を見て
取った場合は
下記(2)のr=4,s=48,n=52の
Aの場合なので
r/n = 4/52 = 1/13
なので確率は変化なし
という計算結果になりました。
シミュレートでも同じような結果
になりました
考える度に、本当に合っているのか?
と疑問に思ってしまいます
それぞれ〇がr個,×がs個入ったn≧2個の箱がある。
A,Bの順で選びBの結果後Cが選ぶ。
次の場合、A,Cの箱が〇である確率を求める。
(1) Bが開けると×の時(無作為に選ぶ)
(2) Bが必ず×を選ぶ時(中を見て選ぶ)
(3) Bが開けると〇の時(無作為に選ぶ)
(4) Bが必ず〇を選ぶ時(中を見て選ぶ)
Aが〇,×をA,AXとする
Bが〇の条件でAが〇の確率をPB(A)、
Aの後Bが〇の条件でCが〇をPB(C)
と書く事にする
箱が2個の時はCは取れないので
P(C) = 0
です
Bが無作為に選ぶ時
P(A~C) = r/n, P(AX~CX) = s/n
PB(A) = {P(A)∩P(B)}/P(B)
= (r/n){(r-1)/(n-1)} / (r/n) = (r-1)/(n-1)
PBX(A) = {P(A)∩P(BX)}/P(BX)
= (r/n){s/(n-1)} / (s/n) = r/(n-1)
Bが×を選ぶ時
P(A,C) = r/n, P(AX,CX) = s/n
P(B) = 0, P(BX) = 1
PBX(A) = {P(A)∩P(BX)}/P(BX) = (r/n) / 1
= r/n (if s > 1), 1 (if s = 1)
Bが〇を選ぶ時
P(A,C) = r/n, P(AX,CX) = s/n
P(B) = 1, P(BX) = 0
PB(A) = {P(A)∩P(B)}/P(B) = (r/n) / 1
= r/n (if r > 1), 0 (if r = 1)
表を使って考える
以下、A,B,Cの順に確率の積をO,Xの後に
表記しています
(1)(3) Bが開けるとX,O [下記ab/cd = (ab)/(cd)とする]
A | B | C結果 | B-AC |
O r/n | O r(r-1)/n(n-1) | O r(r-1)(r-2)/n(n-1)(n-2) | O-OO |
|
| X r(r-1)q/n(n-1)(n-2) | O-OX |
| X rq/n(n-1) | O rq(r-1)/n(n-1)(n-2) | X-OO |
|
| X rq(q-1)/n(n-1)(n-2) | X-OX |
X q/n | O qr/n(n-1) | O qr(r-1)/n(n-1)(n-2) | O-XO |
|
| X qr(q-1)/n(n-1)(n-2) | O-XX |
| X q(q-1)/n(n-1) | O q(q-1)r/n(n-1)(n-2) | X-XO |
|
| X q(q-1)(q-2)/n(n-1)(n-2) | X-XX |
P(BX) = rq/n(n-1) + q(q-1)/n(n-1)
= q(r+q-1)/{n(n-1)} = q/n
PBX(A) = (X-OO + X-OX)/P(BX)
= {rq(r-1)+rq(q-1)}/{n(n-1)(n-2)}/(q/n)
= {r(r-1)+r(q-1)}/{(n-1)(n-2)}
= r(r+q-2)/{(n-1)(n-2)} = r/(n-1)
PBX(C) = (X-OO + X-XO)/P(BX)
= (X-OO + X-OX)/P(BX) = PBX(A) = r/(n-1)
P(B) = r(r-1)/n(n-1) + qr/n(n-1)
= r(r-1+q)/{n(n-1)} = r/n
PB(A) = (O-OO + O-OX)/P(B)
= {r(r-1)(r-2) + r(r-1)q}/{n(n-1)(n-2)}/(r/n)
= (r-1)(r-2+q)/{(n-1)(n-2)} = (r-1)/(n-1)
PB(C) = (O-OO + O-XO)/P(B)
= (O-OO + O-OX)/P(B) = PB(A) = (r-1)/(n-1)
(2) Bが必ずXを選ぶ [下記ab/cd = (ab)/(cd)とする]
A | B | C結果 | B-AC |
O r/n | X r/n | O r(r-1)/n(n-2) | X-OO |
|
| X r(q-1)/n(n-2) | X-OX |
X q/n | X q/n | O qr/n(n-2) | X-XO |
|
| X q(q-2)/n(n-2) | X-XX |
P(BX) = 1
PBX(A) = (X-OO + X-OX)/P(BX)
= {r(r-1)+r(q-1)}/{n(n-2)}/1
= r(r+q-2)/{n(n-2)}
= r/n (1 if q≦1)
PBX(C) = (X-OO + X-XO)/P(BX)
= {r(r-1)+qr}/{n(n-2)}/1
= r(r-1+q)/{n(n-2)}
= r(n-1)/{n(n-2)} (1 if q≦1)
ただし、この時のPBX(A)はBがXを選べた
条件での確率なので、q≦1の時はXは
残っていないので、PBX(A) = PBX(C) = 1
です
(4) Bが必ずOを選ぶ [下記ab/cd = (ab)/(cd)とする]
A | B | C結果 | B-AC |
O r/n | O r/n | O r(r-2)/n(n-2) | O-OO |
|
| X rq/n(n-2) | O-OX |
X q/n | O q/n | O q(r-1)/n(n-2) | O-XO |
|
| X q(q-1)/n(n-2) | O-XX |
P(B) = 1
PBX(A) = (O-OO + O-OX)/P(B)
= {r(r-2)+rq}/{n(n-2)}/1
= r(r-2+q)/{n(n-2)}
= r/n (0 if r≦1)
PBX(C) = (O-OO + O-XO)/P(BX)
= {r(r-2)+q(r-1)}/{n(n-2)}/1
= (rr-r-r+qr-q)/{n(n-2)}
= {r(r+q)-r-(r+q)}/{n(n-2)}
= (rn-r-n)/{n(n-2)} (0 if r≦1)
ただし、この時のPBX(A)はBがOを選べた
条件での確率なので、r≦1の時はOは
残っていないので、PBX(A) = PBX(C) = 0
です
NL-BASICとblg~.zip(monty003.bas)は
このブログ(以下のリンク)から
ダウンロードできます
https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい