N88-BASICでモンティホール問題 (4回目) (3囚人問題)
2021/12/16(木)
N88-BASICでモンティホール問題 (4回目)
(Monty Hall problem)
モンティーホール問題と似た問題
3囚人問題
(Three Prisoners problem)
A,B,Cの3死刑囚の内1人が恩赦を受ける
Aは看守にB,Cどちらかは死刑になるのだから
どちらか教えてほしいと言う
看守はBは死刑になると教えてくれた
Aが助かる確率は上がったか、という問題
(選択はすべて等確率で起こるとする)
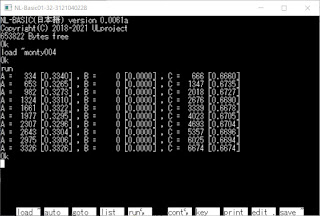
シミュレート結果は
Aはほぼ1/3(=0.33..)、
Bは当然Bが死刑になると看守が言っているので0、
Cはなぜかほぼ2/3(0.66..)、
となり、
看守からBが死刑になると聞いても
Aが助かる確率は変わらないという
結果になりました
不思議です...
が、よく考えてみると、
|
|
|
|
| B決定後 | |||
A | B | C | 聞く前 | 看守の答 | A | C | ||
○ | × | × | 1/3 | 恩赦 | 1/6 | B | 恩赦 | 死刑 |
1/6 | C |
|
| |||||
× | ○ | × | 1/3 | 死刑 | 1/6 | C |
|
|
1/6 | C |
|
| |||||
× | × | ○ | 1/3 | 死刑 | 1/6 | B | 死刑 | 恩赦 |
1/6 | B | 死刑 | 恩赦 | |||||
恩赦がAの時、看守はB or Cを答える(BとCで1/3)
恩赦がBの時、看守はC or Cを答える(Cは1/3)
恩赦がCの時、看守はB or Bを答える(Bは1/3)
よって、上記表の様になります
看守はBが死刑とAに教えたので、
上記表の内、Bと答えている事象
しか起きていないので、
Aは1/3、Cは2/3で恩赦となる
(Bは0/3で恩赦になる)
1/3の確率が変化したのはB,Cとなります
問題は、看守の選択肢にAが無く
B or Cで聞いているので、
B,Cの確率が変化したのだと思います
(ここは何かすっきりしませんが...)
では、看守にA,B,Cの誰が死刑か答えてもらい、
Bと答えたとすると、
|
|
|
|
| B決定後 | |||
A | B | C | 聞く前 | 看守の答 | A | C | ||
○ | × | × | 1/3 | 恩赦 | 1/6 | B | 恩赦 | 死刑 |
1/6 | C |
|
| |||||
× | ○ | × | 1/3 | 死刑 | 1/6 | A |
|
|
1/6 | C |
|
| |||||
× | × | ○ | 1/3 | 死刑 | 1/6 | A |
|
|
1/6 | B | 死刑 | 恩赦 | |||||
AもCも1/2で恩赦となり、
A,B,Cすべての確率が変わりました
3囚人問題は
モンティーホール問題と
同じです
NL-BASICとblg~.zip(monty004.bas)は
このブログ(以下のリンク)からダウンロードできます
https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい