N88-BASICでユークリッドの互除法
2022/2/21(月)
N88-BASICでユークリッドの互除法
最大公約数を求めて分数を約分する
ユークリッドの互除法(Euclidean Algorithm)
a ∈ Z は、aは整数という意味(Zは二重線文字)
(Z:整数 Q:有理数 R:実数 C:複素数)
最大公約数はGCD(Greatest Common Divisor)
なので、ここでは、GCD(a, b)と表すことにする
a, b, n, r ∈ Z
a > b > 0
a / b = n … r
とすると、
GCD(a, b) = GCD(b, r)
が成り立ちます
N88-BASICでユークリッドの互除法
a ∈ Z は、aは整数という意味(Zは二重線文字)
(Z:整数 Q:有理数 R:実数 C:複素数)
最大公約数はGCD(Greatest Common Divisor)
なので、ここでは、GCD(a, b)と表すことにする
a > b > 0
a / b = n … r
とすると、
GCD(a, b) = GCD(b, r)
が成り立ちます
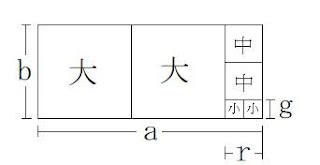
図1 正方形1辺の長さ大=b,中=r,小=g
a / b の余りはr
b / r の余りはg
r / g の余りは0
よって、図1を見ると、
r = 2g
b = 2r + g = 4g + g = 5g
a = 2b + r = 8g + 2g = 12g
となり、
gはa,bの、大きいほうから初めに見つけた
公約数になっているので、最大公約数です
図1によると、
GCD(a, b) = GCD(b, r) = GCD(r, g) = g です
↑ ↑
a / bの余り > 0 r / gの余り = 0
よって、アルゴリズムは、
(1) a / b の余りrを求める(a > b > 0)
(2) a = b, b = r
(3) b > 0なら(1)へ
(4) aが答え
約分は
A > 0, B > 0, G = GCD(A, B)として、
A / B = (A/G) / (B/G)
負数の場合は絶対値に対して計算し
後で符号を付ければ良いと思います
NL-BASICとblg~.zip(euc001.bas)は
以下のリンクからダウンロードできます