N88-BASICで点と直線の距離 (2回目)

2022/3/27(日)
N88-BASICで点と直線の距離 (2回目)

円が切取る線分の長さ

 
原点を中心とする半径r円が
直線ax+by+c=0を切断する長さsを
求めます
 
 

 

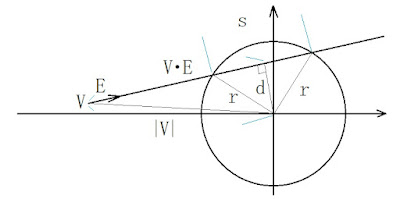
図1.
 
原点以外の中心(x₁,y₁)の円の場合
円と直線を移動して中心を原点に持ってくれば
(cをax1+by1+cで置換える)よいので説明を
省きます
 
直線L: ax + by + c = 0 [ y = -(a/b)x - c/b ]と
原点との距離d = |c| / √(a²+b²)と半径rから

三平方の定理を使用して
s = 2√(r²-d²) = 2√{r² - c²/(a²+b²)}
 
原点との距離dを求める式は、このブログの
 
N88-BASICで点と直線の距離 (1回目)
を参照して下さい
 

別解

ベクトル表記(大文字をベクトルとする)
直線P = V + Et
円　|P| = r
|E| = 1とすると
(V + Et)･(V + Et) = r² 
|E|²t² + 2(V･E)t + V･V - r² = 0
t² + 2(V･E)t + |V|² - r² = 0
t = -(V･E)±√{(V･E)² - |V|² + r²}
t = -(V･E)±√[r² - {|V|² - (V･E)²}]
これは視点Vから交点までの距離tを求める式で
レイトレーシングで説明した式です
 
https://ulprojectmail.blogspot.com/2021/06/n88-basic-1.html
N88-BASICでレイトレーシング (1回目)

～
 
ベクトル表記の為2次元でも3次元でも
求めることが出来ます
(2次元の円は3次元では球になります)
 
t = -(V･E)±√[r² - {|V|² - (V･E)²}]
が直線と円の交点までの距離なので
円によって切り取られた線分の長さsは
±√[r² - {|V|² - (V･E)²}]
の部分なので
s = 2√[r² - {|V|² - (V･E)²}]
となります
ちなみに
図1、三平方の定理(ピタゴラスの定理)、
原点と直線の距離dの公式より
|V|² - (V･E)² = d² = c²/(a²+b²)
(dは円の中心から直線までの距離)
となる事が分かります

例
10x-10y+100=0 (y=x+10) r=10
中心の距離d = |c|/√(a²+b²) = 100/√{10²+(-10)²}
= 100/√200 = 100/10√2 = 10/√2
d = 5√2
線分の長さs = 2√{r² - c²/(a²+b²)} = 2√(r²-d²)
= 2√{10²-(5√2)²} = 2√(100-50) = 2√50
s = 10√2

 
NL-BASICとblg～.zip(dis002.bas)は

以下のリンクからダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい