N88-BASICでベクトル (1回目)

2022/3/3(木)

N88-BASICでベクトル (1回目)

 
ベクトルの内積
 

 
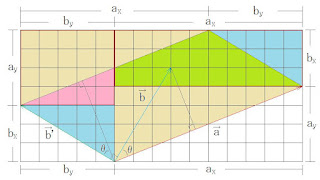
図1 a･b = a_xb_x + a_yb_y
 
ベクトルaとbの内積はa･b = |a||b|cosθ
なので，|b|をaに垂直に落とした陰の長さ
|b|cosθと|a|の積になり、ベクトルbを
90°回転したベクトルb'とaが作る
平行四辺形の面積と考える事が出来ます
|b|cosθ=|b'|cosθ=平行四辺形の高さ
|a|が底辺です
 
図1を見ると、a_xb_x + a_yb_y が平行四辺形の
面積と同じなので、a･b = a_xb_x + a_yb_y と
なります(黄色同士と水色同士を見る)
(a,b,b'ベクトルの成分はマス目の数を
見ると分かり易いと思います)
 
別の導き方、
ここから、ベクトルを大文字で表し、
A=(a₀,a₁,a₂)と成分表記する事にします
E_iを各(直交)座標軸の単位ベクトルとすると、
A = Σa_iE_i 、E_i･E_i = 1 、E_i･E_j = 0(i≠j)
A･B = (Σa_iE_i)･(Σb_iE_i) = Σa_ib_i
となり、各ベクトルの同じ成分同士の積の和
になります
3次元なら、a･b = a_xb_x+a_yb_y+a_zb_z です
A･B = |a||b|cosθより、cosθ = A･B/(|a||b|)
なので、cosの逆関数を使えば2つのベクトルの
なす角がわかります
N88-BASICではtanの逆関数しかないので、
tanθ = sinθ/cosθ
      = √{(1-cosθcosθ)/(cosθcosθ)}
      = √{1/(cosθcosθ) - 1}
      = √[|a||b||a||b|/{(A･B)(A･B)} - 1]
を使用します
a･b    = a_xb_x + a_yb_y
|a||a| = a_xa_x + a_ya_y
|b||b| = b_xb_x + b_yb_y
からx = tanθを求めて、
t  = Tan^-1(x)で角度tが求まります
tがラジアンの場合
θ = 180t/πで角度θ(°)が求まります
ただし、|a||b|=0なら角度不明
a･b < 0の時は180-θです
 
また
Tan^-1(1) = π/4を利用してπを求める事ができます
 
Tan^-1(x)はBASICではATN(X)です
 
以下のサンプルは、
マウスの左クリックでベクトルB
      右クリックでベクトルA
が移動して、なす角が表示されます
 
NL-BASICとblg～.zip(vec001.bas)は
以下のリンクからダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい