N88-BASICでネイピア数 (4回目)

2022/8/15(木)
N88-BASICでネイピア数 (4回目)
 
ネイピア数e(Napier's constant)
 
e^x = lim[n→∞] (1 + x/n)ⁿ 
を変形する
 
(a + b)ⁿ = Σ_nC_ia^n-ibⁱ [i = 0～n] と
nCr = n(n-1)…(n-r+1)/r! より
 
(1 + x/n)ⁿ 
= Σ_nC_i(x/n)ⁱ [i = 0～n]
= 1 + n (x/n) + n(n-1)/2! (x/n)² 
+ n(n-1)(n-2)/3! (x/n)³ + …
 
= 1 + x + (n-1)/2! (x/n) + (n-1)(n-2)/3! (x/n)² + …
= 1 + x + (n-1)/2! (x/n) + (n²-3n+1)/3! (x/n)² + …
= 1 + x + {1/2! - 1/(2!n)}x² 
+ {1/3! - 3/(3!n) + 1/(3!n²)}x³ + …
 
= 1 + x + x²/2! + x³/3! + … (n→∞)
= x⁰/0! + x¹/1! + x²/2! + x³/3! + … (n→∞)
 
lim[n→∞] (1 + x/n)ⁿ 
= Σ(1/k!)x^k [k = 0～∞]
 
結果
e^x = lim[n→∞] (1 + x/n)ⁿ = Σ(1/k!)x^k [k = 0～∞]
 
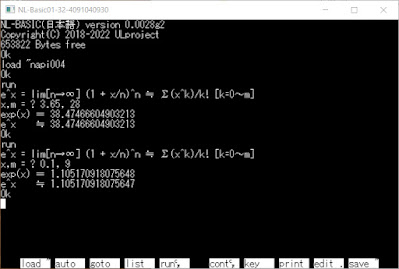
プログラムではmを入力し
e^x = lim[n→∞] (1 + x/n)ⁿ ≒ Σ(1/k!)x^k [k = 0～m]
の計算結果を表示しています
 
 
追記
e^x はexp(x)とも表記し
BASICではexp(x)を使用しa^xはa^xと記述します
 
 
VL,NL,XL-BASICとblg～.zip(napi004.bas)は
以下のリンク)からダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい