天体の軌道(Kepler) (5回目)

2021/10/14(木)

天体の軌道(Kepler) (5回目)

楕円軌道の

tan(f/2) = √{(1+e)/(1-e)}tan(u/2)と

M = u - esinu ケプラー方程式の導出

(真近点角f,離心近点角u,平均近点角M)

 

(fはr=ℓ/(1+ecosf)で楕円を表すときの角です)

(uはx=acosu,y=bsinuで楕円を表すときの角です)

(Mは時間経過を表す角です)

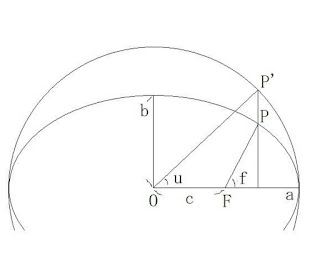
図1. 離心近点角u、真近点角f

 

離心率  e = c / a = c / (q + c)

近点距離q = a(1 - e) = a - c

遠点距離Q = a(1 + e) = a + c

焦点距離c = ae

長半径  a = q / (1 - e) = q + c

短半径  b = √(a² - c²) = a√(1 - e²)

半直弦　ℓ = a(1 - e²) = q(1 + e)

真近点角f

動径　　r = ℓ / (1 + e cosf)

 

焦点Fを原点として、図1の点P(x,y)を

uで表し、楕円を(r,u)で表す。

x'= acosu - c

y'= asinu

x =      x'= acosu - c = rcosf

y = (b/a)y'= bsinu     = rsinf

r² = x²+y² = (acosu - c)² + (bsinu)² 

= a²cos²u - 2accosu + c² + (a²-c²)(1-cos²u)

= -2accosu + a² + c²cos²u

= (a - ccosu)² 

= (a - aecosu)² 

= a²(1 - ecosu)²  … 0≦e＜1, 1-ecosu>0より

r = a(1 - ecosu) > 0 … ①

 

楕円の式

r = a(1 - e²) / (1 + e cosf)を変形し

ecosf = a(1 - e²) / r - 1に①式を代入

      = a(1 - e²) / a(1 - ecosu) - 1

      = (1 - e²) / (1 - ecosu) - 1

      = {(1-e²)-(1-ecosu)}/(1-ecosu)

      = (ecosu - e²) / (1 - ecosu)

cosf = (cosu - e) / (1 - ecosu) … ②

 

加法定理

sin(α±β) = sinαcosβ±cosαsinβ

cos(α±β) = cosαcosβ∓sinαsinβ

については

https://ulprojectmail.blogspot.com/2021/09/1.html

三角関数 (1回目)

を参照して下さい

 

cos2α = cos(α+α) = cos²α-sin²α

= cos²α-(1 - cos²α) = 2cos²α - 1

= (1 - sin²α)-sin²α = 1 - 2sin²α

sin²(α/2) = (1 - cosα)/2

cos²(α/2) = (1 + cosα)/2

 

②式に適用

cosf = (cosu - e) / (1 - ecosu)

sin²(f/2) = {1 - (cosu-e)/(1-ecosu)} / 2

         = {(1-ecosu)-(cosu-e)}/{2(1-ecosu)}

         = (1-ecosu-cosu+e)/{2(1-ecosu)}

         = (1+e){(1-cosu)/2}/(1-ecosu)

         = (1+e)/(1-ecosu) × sin²(u/2)

cos²(f/2) = {1 + (cosu-e)/(1-ecosu)} / 2

         = {(1-ecosu)+(cosu-e)}/{2(1-ecosu)}

         = (1-ecosu+cosu-e)/{2(1-ecosu)}

         = (1-e){(1+cosu)/2}/(1-ecosu)

         = (1-e)/(1-ecosu) × cos²(u/2)

tan(f/2) = √{(1+e)/(1-e)}tan(u/2)

 

次にケプラー方程式 M = u - esinuの導出です

 

惑星の楕円軌道

r = a(1-e²)/(1+ecosf) … (0≦e＜1)

で、角f地点の時間tを、

tan(f/2) = √{(1+e)/(1-e)}tan(u/2)より、

tan(u/2) = √{(1-e)/(1+e)}tan(f/2)と、

ケプラー方程式 M = u - esinuと、

平均近点角M = nt (時間に比例する角度)

で、求めることができる。

 

ただし、時間から位置を求めるときは、

ケプラー方程式を数値計算する必要が

あります。

 

ケプラー方程式の導出

 

時間t、公転周期P(一周する時間)

一周M=2π、t=P ⇒ 2π=nP より

平均運動n = 2π/P

 

前回より、

ℓ = a(1-e²) = b²/a

r = ℓ/(1+ecosf) = a(1-ecosu)

離心近点角u、真近点角f

y = rsinf = bsinu

sinf = (b/r)sinu

  0≦θ<<1なら

  rsinθ < rθ(円弧)、面積r²θ/2 < (rtanθ)/2

  よりsinθ < θ < tanθをsinθで割る

  1 < θ/sinθ < 1/cosθの逆数

  cosθ < (sinθ)/θ < 1

  (sinθ)/θ = 1 (θ→0)

  sinθ = θ (θ<<1)より

sindf = (b/r)sinu ⇒ df = (b/r)du

 

楕円軌道の面積速度一定の法則より、

面積速度K = const.(一定)

楕円は半径aの円(面積πa²)をb/aに潰した

ものなので、楕円の面積S = πab

(a:長半径、b:短半径)

M = nt = 2πの時のt = 2π/n

K = S/t = πab/(2π/n) = nab/2

角dfの掃引面積をdSとすると、

面積速度dS/dt = K = nab/2 (一定)

 

扇の面積=πr²(θ/2π)=θr²/2

f << 1(十分小さい)ときのfをdfとすると

角dfの掃引面積dSは扇に近づくと考えて、

dS = df(r²/2)にdf = (b/r)duを代入して、

dS = (br/2)du

dS/dt = (br/2)(du/dt) = K = nab/2

(r/a)(du/dt) = nにr = a(1-ecosu)

を代入して両辺tで積分すると、

∫(1-ecosu)(du/dt)dt = ∫ndt

∫(1-ecosu)du = ∫ndt

u-esinu = nt + C

t = 0の時u = 0なら積分定数C = 0

M = nt より、

ケプラー方程式 M = u - esinu

が導かれる