N88-BASICで3次方程式 (3回目)

2021/10/9(土)
N88-BASICで3次方程式 (3回目)
 
ax3 + bx2 + cx + d = 0の解を
Re y = Re(ax3 + bx2 + cx + d)のグラフとの
交点(Re x, Im x, Re y)で表示します
 
Re y = Re(ax3 + bx2 + cx + d)にx = R + Iiを代入
　= Re(a(R3+3R2Ii-3RI2-I3i)+b(R2+2RIi-I2)+c(R+Ii)+d)
　= Re(aR3-3aRI2+bR2-bI2+cR+d + (3aR2-aI2+2bR+c)Ii)
　= aR3-3aRI2+bR2-bI2+cR+d
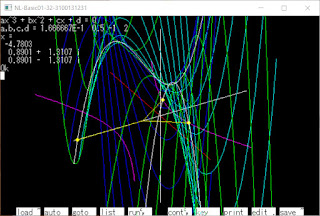
Re y = aR3-3aRI2+bR2-bI2+cR+d
のグラフを立体的に表示しました
 
分かりやすい形を選ぼうとしましたが
なかなか良い形が見つかりませんでした
2次方程式の時よりも分かりにくいので
ご了承下さい
 
横(Re x - Re y平面)からだと3次曲線
前(Im x - Re y平面)からだと放物線
(途中で逆転)に見えています
 
回転行列については、このブログの
https://ulprojectmail.blogspot.com/2021/06/n88-basicmatrix-1.html
N88-BASICで行列(matrix) (1回目)～
を参照して下さい



 







NL-BASICとblg～.zip(cubi003.bas)は
このブログ(以下のリンク)からダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい


このブログの人気の投稿

NEWS

2024/5/11(土 ) メモ (7回目)(哲学と科学) を公開しました    2024/5/5(日 ) N88-BASICで軌跡 を公開しました    2024/4/21(日) VL,NL,XL-BASIC(ver～28u5) を公開しました
続きを読む

N88-BASICでゲーム (1回目)

イメージ
2021/8/16(月) N88-BASICでゲーム  (1回目) by ULproject   球同士の衝突と跳返り   大文字ベクトル、小文字スカラー 文字の後の、 'は衝突後、数字は球番号   球同士の反発係数、衝突面に水平 ,垂直u,e 球の中心位置 P,半径r,質量m,速度V 衝突面の球 1方向の法線N = (P 1 -P 2 )/|P 1 -P 2 |   球同士の衝突は、 |P 1 -P 2 | ≦ r 1 +r 2   なので √{(P 1 -P 2 )･(P 1 -P 2 )} ≦ r 1 +r 2   (P 1 -P 2 )･(P 1 -P 2 ) ≦ (r 1 +r 2 )(r 1 +r 2 ) で判断できます。   ここで、ベクトルの計算ですが、 P(i) (i=0,1,2) をPのx,y,z成分と すると、 P = P 1  - P 2 は、 P(i) = P1(i) - P2(i) (i=0,1,2) P･Pは ΣP(i)P(i) (i=0,1,2) となります   BASICでは、 P(0) = P1(0) - P2(0) P(1) = P1(1) - P2(1) P(2) = P1(2) - P2(2) D = P(0)*P(0)+P(1)*P(1)+P(2)*P(2) R = R1 + R2 IF D <= R*R THEN 重なり又は接触 となります。   反発させるときは、球が接触している 間は再び反発しないようにしないと 球が離れなくなります。   次に反発についてですが、衝突面に 水平な成分は、球の回転に関係します が、ここでは球の回転は考えずに 垂直成分と同じように反発係数で 減速させる事にします。   衝突面に垂直な成分 (v 1 は球 1の速度、v 1 'は衝突後) 運動量 p = mv 運動量保存則 p 1 +p 2 =p 1 '+ p 2 'より p 1 +p 2  = m 1 v 1 '+ m 2 v 2 ' 反発係数 e = -(v 1 '- v 2 ')/(v 1  - v 2 )より ev 1  - ev 2  = -v 1 '+ v 2 '     em 2 v 1  - em 2 v 2  = -m 2 v 1 
続きを読む