N88-BASICでネイピア数 (3回目)

2022/9/12(月)
N88-BASICでネイピア数 (3回目)
 
ネイピア数e(Napier's constant)
 
年利x (100x %) の利息について、1年をn等分して
複利で1年後の残金が何倍になるかを計算すると
 
n = 1 → 1+x
n = 2 → (1+x/2)(1+x/2) = (1+x/2)² 
となるのでn等分の場合
(1 + x/n)ⁿ 倍になる
 
https://ulprojectmail.blogspot.com/2022/09/n88-basicnapier-1.html
N88-BASICでネイピア数 (1回目)
より
e = lim[n→∞] (1 + 1/n)ⁿ 
を使用して
lim[n→∞] (1 + x/n)ⁿ 
をeで表す
 
n/x = hと置くとn→∞のときh→∞
n = xhなので
lim[n→∞] (1 + x/n)ⁿ 
= lim[h→∞] (1 + 1/h)^hx 
= { lim[h→∞] (1 + 1/h)^h }^x 
　ここで「lim[n→∞] (1 + 1/n)ⁿ = e」より
= e^x 
となる
 
プログラムではnを入力し
a = (1 + x/n)ⁿ をe^x = exp(x)と共に
表示しています
 
 
ちなみに
 
10日で1割ならば1年(複利)で33倍近くになり
1日で1％ならば1年(複利)で38倍近くになります
 
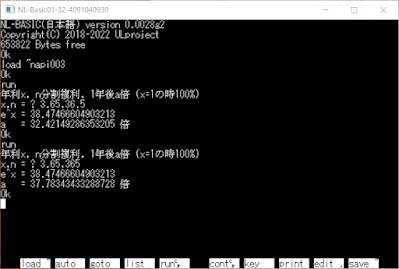
年利x=0.1/10×365=3.65, 分割n=365/10=36.5
年利x=0.01×365  =3.65, 分割n=365で、それぞれ
32.42149286353205
37.78343433288728
と表示されます
 
 
より正確に計算するならば
現在のカレンダーに使用されている暦(グレゴリオ暦)
の1年を近似した365.2425日を使用して下さい
 
グレゴリオ暦については
https://ulprojectmail.blogspot.com/2021/09/n88-basicjd-1.html
N88-BASICでユリウス日(JD) (1回目)
を参照して下さい
 
 
VL,NL,XL-BASICとblg～.zip(napi003.bas)は
以下のリンク)からダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい