N88-BASICで二項分布 (1回目)
2021/11/9(火)
N88-BASICで二項分布 (1回目)
二項分布(Binomial distribution)とは
独立試行の事象Aが確率pで起こるとする
n回の独立試行でAが起こった回数Xとその確率P
の確率分布を二項分布といいB(n, p)で表す
(X-Pのグラフは確率分布を表す)
また、B(n, p)のときX=rとなる確率Pは
nCrpr(1-p)n-r となります
組合せnCr(Combination)については
https://ulprojectmail.blogspot.com/2021/11/n88-basicpc.html
N88-BASICで順列組合せ
を参照して下さい
二項分布B(n, p)のときX=rとなる
確率P = nCrpr(1-p)n-r の解説
例、サイコロを3回投げて2回2以下が出る確率は
試行回数n, 1回の試行で事象が起こる確率pより
n = 3, p = 1/3の二項分布B(3, 1/3)に従う
3C2(1/3)2(2/3)1 = 3・2/(2・1)・2/33 = 2/32 = 2/9
解説
サイコロの目が2以下の時〇それ以外を×で表すと
1回目|2回目|3回目|
〇(1/3)|〇(1/3)|〇(1/3)|
〇(1/3)|〇(1/3)|×(2/3)|=(1/3)(1/3)(2/3)=(1/3)2(2/3)1
〇(1/3)|×(2/3)|〇(1/3)|=(1/3)(2/3)(1/3)=(1/3)2(2/3)1
〇(1/3)|×(2/3)|×(2/3)|
×(2/3)|〇(1/3)|〇(1/3)|=(2/3)(1/3)(1/3)=(1/3)2(2/3)1
×(2/3)|〇(1/3)|×(2/3)|
×(2/3)|×(2/3)|〇(1/3)|
×(2/3)|×(2/3)|×(2/3)|
〇が2回、×が1回起こる確率は(1/3)2(2/3)1 = 2/27
〇が2回、×が1回の組合せは
(〇の順は考えないので順列ではない)
3個中2個〇を選ぶ選び方と同じなので
3C2 = 3通り(上記図でも3通りと分かる)
なので
3C2(1/3)2(2/3)1 = 3・2/27 = 2/9 = 0.222…
試行回数n=3, 事象A(〇である)の回数r=2
事象Aの確率p=1/3, 1-p=2/3とすると
3C2(1/3)2(2/3)1 = nCrpr(1-p)n-r となる
二項分布の平均と標準偏差
平均と標準偏差は
https://ulprojectmail.blogspot.com/2021/11/n88-basicsd.html
N88-BASICで偏差値
を参照して下さい
確率分布の期待値E(X)(平均m)は
確率分布が
X x1 x2 … xn 計
P p1 p2 … pn 1
の時
E(X) = x1p1 + x2p2 + … + xnpn
となる
例えば、サイコロを投げた時
p = 1/6
X 1 2 3 4 5 6 計
P p p p p p p 1
E(X) = 1p + 2p + … + 6p
= (1+2+…+6)/6 = 21/6 = 7/2 = 3.5
となり、通常の平均と同じ計算になる
以後確率変数XとYが独立であるとする
(くじを引いてXが当たりかはずれに
よって次引く人Yの確率が変わる場合
XとYは独立ではない
くじを引いてXが当たりかはずれか見て
戻すと次引く人Yの確率は変わらないので
XとYは独立となる)
ΣXP=Σxipi ,ΣYQ=Σyiqi(i=1~n)とすると
E(X+Y) = Σ(XP+YQ) = ΣXP+ΣYQ
= E(X)+E(Y)
E(aX) = Σ(aXP) = aΣXP = aE(X)
E(XY) = ΣΣ(XPYQ) (各xipiで括ると)
= ΣXPΣYQ = E(X)E(Y)
V(X+Y) = E((X+Y)2) - {E(X+Y)}2
V(X+Y) = E(X2+Y2+2XY) - {E(X)+E(Y)}2
= E(X2)-{E(X)}2 + E(Y2)-{E(Y)}2
+ E(2XY)-2E(X)E(Y)
= V(X) + V(Y) + E(2XY)-E(2XY)
= V(X) + V(Y)
独立試行の事象Aが確率pで起こるとする
n回の独立試行でAが起こった回数Xとその確率P
の確率分布を二項分布といいB(n, p)で表す
X-Pのグラフが確率分布を表す
また、B(n, p)のときX=rとなる確率Pは
nCrpr(1-p)n-r となる
独立試行の事象Aが確率pで起こるとする
(Aが起こらない確率をqとするとq=1-p)
n回の独立試行でAがi回目に起こった時
Xi=1起こらなければXi=0となる確率変数
Xi(i=1~n)を考える
1回 2回 … n回目
X1 + X2 + … + Xn = Xとなる
Xiの確率分布は
Xi 0 1 計
P q p 1
よって
期待値E(Xi) = 0q+1p = p
期待値E(Xi2) = 02q+12p = p
分散V(Xi) = E(Xi2)-{E(Xi)}2
= p - p2 = p(1-p) = pq
期待値E(X) = ΣE(Xi)(i=1~n)
= E(X1)+…+E(Xn) = np
Xiは互いに独立(互いの確率に影響がない)
なので
分散V(X) = ΣV(Xi)(i=1~n)
= npq
標準偏差σ(X) = √(npq)
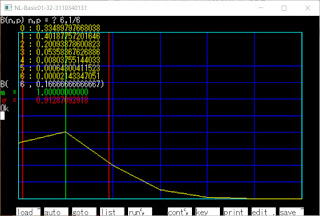
プログラムではグラフで表示しています
B(n,p)=B(6,1/6)の入力では
サイコロ6回振って1が出る回数毎の
確率が表示されr=0のとき約33%(0.33...)
つまり1が1回も出ない確率が33%もある
事が分かります
この事は、コインを2回投げて表が1回も
出ない確率は裏裏と出る確率なので
(1/2)・(1/2) = 1/4 = 0.25となるのは
簡単に理解できると思います
1/2の表が2回投げても出ない確率は
意外と高いです
1/100の確率で当たるルーレットを
100回しても
100C0(1/100)0(1/100)99 ≒ 0.366032...
37%ほど1回も当たらないのです
さすがに1回ぐらいは当たるだろうと
思っていたら大損するということです
NL-BASICとblg~.zip(bino001.bas)は
このブログ(以下のリンク)から
ダウンロードできます
二項分布(Binomial distribution)とは
独立試行の事象Aが確率pで起こるとする
n回の独立試行でAが起こった回数Xとその確率P
の確率分布を二項分布といいB(n, p)で表す
(X-Pのグラフは確率分布を表す)
また、B(n, p)のときX=rとなる確率Pは
nCrpr(1-p)n-r となります
組合せnCr(Combination)については
https://ulprojectmail.blogspot.com/2021/11/n88-basicpc.html
N88-BASICで順列組合せ
を参照して下さい
二項分布B(n, p)のときX=rとなる
確率P = nCrpr(1-p)n-r の解説
例、サイコロを3回投げて2回2以下が出る確率は
試行回数n, 1回の試行で事象が起こる確率pより
n = 3, p = 1/3の二項分布B(3, 1/3)に従う
3C2(1/3)2(2/3)1 = 3・2/(2・1)・2/33 = 2/32 = 2/9
解説
サイコロの目が2以下の時〇それ以外を×で表すと
1回目|2回目|3回目|
〇(1/3)|〇(1/3)|〇(1/3)|
〇(1/3)|〇(1/3)|×(2/3)|=(1/3)(1/3)(2/3)=(1/3)2(2/3)1
〇(1/3)|×(2/3)|〇(1/3)|=(1/3)(2/3)(1/3)=(1/3)2(2/3)1
〇(1/3)|×(2/3)|×(2/3)|
×(2/3)|〇(1/3)|〇(1/3)|=(2/3)(1/3)(1/3)=(1/3)2(2/3)1
×(2/3)|〇(1/3)|×(2/3)|
×(2/3)|×(2/3)|〇(1/3)|
×(2/3)|×(2/3)|×(2/3)|
〇が2回、×が1回起こる確率は(1/3)2(2/3)1 = 2/27
〇が2回、×が1回の組合せは
(〇の順は考えないので順列ではない)
3個中2個〇を選ぶ選び方と同じなので
3C2 = 3通り(上記図でも3通りと分かる)
なので
3C2(1/3)2(2/3)1 = 3・2/27 = 2/9 = 0.222…
試行回数n=3, 事象A(〇である)の回数r=2
事象Aの確率p=1/3, 1-p=2/3とすると
3C2(1/3)2(2/3)1 = nCrpr(1-p)n-r となる
二項分布の平均と標準偏差
平均と標準偏差は
https://ulprojectmail.blogspot.com/2021/11/n88-basicsd.html
N88-BASICで偏差値
を参照して下さい
確率分布の期待値E(X)(平均m)は
確率分布が
X x1 x2 … xn 計
P p1 p2 … pn 1
の時
E(X) = x1p1 + x2p2 + … + xnpn
となる
例えば、サイコロを投げた時
p = 1/6
X 1 2 3 4 5 6 計
P p p p p p p 1
E(X) = 1p + 2p + … + 6p
= (1+2+…+6)/6 = 21/6 = 7/2 = 3.5
となり、通常の平均と同じ計算になる
以後確率変数XとYが独立であるとする
(くじを引いてXが当たりかはずれに
よって次引く人Yの確率が変わる場合
XとYは独立ではない
くじを引いてXが当たりかはずれか見て
戻すと次引く人Yの確率は変わらないので
XとYは独立となる)
ΣXP=Σxipi ,ΣYQ=Σyiqi(i=1~n)とすると
E(X+Y) = Σ(XP+YQ) = ΣXP+ΣYQ
= E(X)+E(Y)
E(aX) = Σ(aXP) = aΣXP = aE(X)
E(XY) = ΣΣ(XPYQ) (各xipiで括ると)
= ΣXPΣYQ = E(X)E(Y)
V(X+Y) = E((X+Y)2) - {E(X+Y)}2
V(X+Y) = E(X2+Y2+2XY) - {E(X)+E(Y)}2
= E(X2)-{E(X)}2 + E(Y2)-{E(Y)}2
+ E(2XY)-2E(X)E(Y)
= V(X) + V(Y) + E(2XY)-E(2XY)
= V(X) + V(Y)
独立試行の事象Aが確率pで起こるとする
n回の独立試行でAが起こった回数Xとその確率P
の確率分布を二項分布といいB(n, p)で表す
X-Pのグラフが確率分布を表す
また、B(n, p)のときX=rとなる確率Pは
nCrpr(1-p)n-r となる
独立試行の事象Aが確率pで起こるとする
(Aが起こらない確率をqとするとq=1-p)
n回の独立試行でAがi回目に起こった時
Xi=1起こらなければXi=0となる確率変数
Xi(i=1~n)を考える
1回 2回 … n回目
X1 + X2 + … + Xn = Xとなる
Xiの確率分布は
Xi 0 1 計
P q p 1
よって
期待値E(Xi) = 0q+1p = p
期待値E(Xi2) = 02q+12p = p
分散V(Xi) = E(Xi2)-{E(Xi)}2
= p - p2 = p(1-p) = pq
期待値E(X) = ΣE(Xi)(i=1~n)
= E(X1)+…+E(Xn) = np
Xiは互いに独立(互いの確率に影響がない)
なので
分散V(X) = ΣV(Xi)(i=1~n)
= npq
標準偏差σ(X) = √(npq)
プログラムではグラフで表示しています
B(n,p)=B(6,1/6)の入力では
サイコロ6回振って1が出る回数毎の
確率が表示されr=0のとき約33%(0.33...)
つまり1が1回も出ない確率が33%もある
事が分かります
この事は、コインを2回投げて表が1回も
出ない確率は裏裏と出る確率なので
(1/2)・(1/2) = 1/4 = 0.25となるのは
簡単に理解できると思います
1/2の表が2回投げても出ない確率は
意外と高いです
1/100の確率で当たるルーレットを
100回しても
100C0(1/100)0(1/100)99 ≒ 0.366032...
37%ほど1回も当たらないのです
さすがに1回ぐらいは当たるだろうと
思っていたら大損するということです
NL-BASICとblg~.zip(bino001.bas)は
このブログ(以下のリンク)から
ダウンロードできます