N88-BASICで二項分布 (6回目)

2021/11/14(日)
N88-BASICで二項分布 (6回目)
 

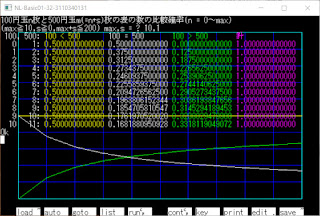
100円玉n枚と500円玉m枚を同時に投げた時
それぞれの表の数をx, yとすると
x < y, x = y, x > y となる確率pを求め
nとpのグラフを表示しました
ただし、n≦mとする
(n＞mの時は硬貨を入替えれば良いため)

 
maxとsを入力し、
n=0～max, m=s～max+s
としています

---------------------------------------------
特別な場合
---------------------------------------------
硬貨の枚数の差m-nが1のとき
x < yの確率(100円の表が少なくなる確率)は、
nにかかわらず0.5になっています

これは、

n枚の100円玉とn+1枚の500円玉を同時に投げて

表の数が100円玉より500円玉のほうが多い確率は?

2005年度・京都大学・理系(後期)

の答えになっています

 
---------------------------------------------
考察
---------------------------------------------
nCrの公式、詳しくは
https://ulprojectmail.blogspot.com/2021/11/n88-basicbnp-3.html
N88-BASICで二項分布 (3回目)
を参照
nCr = n!/{(n-r)!r!} = _nC_n-r 
ΣnCi = 2ⁿ (i=0～n)
 
P(x < y)の式、詳しくは
https://ulprojectmail.blogspot.com/2021/11/n88-basicbnp-5.html
N88-BASICで二項分布 (5回目)
を参照
P(x < y) =
(1/2)^n+m･Σ(mCy･ΣnCx) (内x=0～y-1)(外y=1～n)
+ (1/2)^m･ΣmCy (y=n+1～m)
にm=n+1を代入した式をpとすると
p
= (1/2)²ⁿ⁺¹･Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
+ (1/2)ⁿ⁺¹ 
= (1/2)²ⁿ⁺¹{Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
+ 2ⁿ}
 
ここで
2Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
=Σ(_n+1Cy･ΣnCx) (内x=0～i-1)(外y=i)
+Σ(_n+1Cy･ΣnCx) (内x=0～n+1-i-1)(外y=n+1-i)
(i=1～n)
=Σ(_n+1Cy･ΣnCx) (内x=0～i-1)(外y=i)
+Σ(_n+1Cy･ΣnCx) (内x=0～n-i)(外y=i)
(i=1～n)
=Σ(_n+1Cy･ΣnCx) (内x=0～i-1)(外y=1～n)
+Σ(_n+1Cy･ΣnCx) (内x=n～i)(外y=1～n)
=Σ(_n+1Cy･ΣnCx) (内x=0～n)(外y=1～n)
= 2ⁿΣ_n+1Cy (y=1～n)
よって
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
= 2ⁿ(1/2)Σ_n+1Cy (y=1～n)
= 2ⁿ(1/2)(Σ_n+1Cy - 1 - 1) (y=0～n+1)
= 2ⁿ{(1/2)Σ_n+1Cy - 1} (y=0～n+1)
= 2ⁿ{1/2)2ⁿ⁺¹ - 1}
= 2ⁿ(2ⁿ - 1)
 
p
= (1/2)²ⁿ⁺¹{Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
+ 2ⁿ}
= (1/2)²ⁿ⁺¹{2ⁿ(2ⁿ - 1) + 2ⁿ}
= (1/2)²ⁿ⁺¹(2²ⁿ - 2ⁿ + 2ⁿ)
= (1/2)²ⁿ⁺¹･2²ⁿ 
= 1/2
となります
 
---------------------------------------------
余談
---------------------------------------------
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
= 2ⁿ(1/2)Σ_n+1Cy (y=1～n)
の式変形を思い付いた過程
 
y = 1, y = nのとき簡単になりそう
 
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1)
= Σ(_n+1Cy･ΣnCx) (内x=0～0)(外y=1)
= (n+1)･1
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=n)
= Σ(_n+1Cy･ΣnCx) (内x=0～n-1)(外y=n+1-n=1)
= (n+1)･ΣnCx (x=0～n-1)
= (n+1)(ΣnCx - nCn) (x=0～n)
= (n+1)(2ⁿ - 1) (x=0～n)
 
y = 2, y = n-1のときも簡単になりそう
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=2)
= Σ(_n+1Cy･ΣnCx) (内x=0～1)(外y=2)
= {(n+1)n/2}(1 + n)
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=n-1)
= Σ(_n+1Cy･ΣnCx) (内x=0～n-2)(外y=2)
= {(n+1)n/2}･ΣnCx (x=0～n-2)
= {(n+1)n/2}(ΣnCx - nC_n-1 - nCn) (x=0～n)
= {(n+1)n/2}(2ⁿ - n - 1) (x=0～n)
 
y = (1,n)と(2,n-1)の組同士足すと
(n+1)･2ⁿと{(n+1)n/2}･2ⁿ なので
1,2　,…,n-1,n
n,n-1,…,2　,1
の上段と下段で組を作り
合計を半分にする
 
Σ(_n+1Cy･ΣnCx) (内x=0～y-1)(外y=1～n)
=(1/2){Σ(_n+1Cy･ΣnCx)+Σ(_n+1C_n+1-y･ΣnCx)}
(内x=0～y-1)(外y=1～n)
=(1/2)･2ⁿΣ_n+1Cy (y=1～n)
と導きました
 
---------------------------------------------
他の解き方
---------------------------------------------
100円玉n枚の表の数をx
500円玉n枚の表の数をy'
500円玉m枚の表の数をyとし
確率P(x<y') = P(x>y') = B
P(x=y') = Aと置く(A+2B = 1)
 
m = n + 1のとき
y=y'+1となる確率は1/2なので
x=y'だった場合1/2の確率でx<yとなるため
 
P(x<y) = P(x<y') + (1/2)P(x=y')
= B + A/2 = (1/2)(A+2B) = 1/2
となります
 
ちなみに
P(x=y) = P(x=y') - (1/2)P(x=y')
+ (1/2)P(y'-x=1)
P(x>y) = P(x>y') - (1/2)P(y'-x=1)
C = (1/2)P(y'-x=1)と置いて
 
P(x<y) = P(x<y') + A/2 = 1/2
P(x=y) = P(x=y') - A/2 + C
P(x>y) = P(x>y') - C
です
 
---------------------------------------------
最後に
---------------------------------------------
bino006.basを実行し、maxとsを入力すると
n=0～maxでnとn+s枚での確率pを
n-pグラフで表示し
0～maxまでをmax/10ずつの数値表示がされます
 
範囲を10≦max+s≦200 (max,s≧0)
としていますが適当です
大きいと計算に時間がかかります
 
NL-BASICとblg～.zip(bino006.bas)は
このブログ(以下のリンク)から
ダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい