N88-BASICで楕円 (1回目)

2021/10/22(金)
N88-BASICで楕円 (1回目)
 
極座標系の楕円の式は
https://ulprojectmail.blogspot.com/2021/09/2.html
三角関数 (2回目)
を参照して下さい

極座標系と直交座標系の変換
極座標系⇒直交座標系は、
x = rcosθ (cosθ = x / rより)
y = rsinθ (sinθ = y / rより)
直交座標系⇒極座標系は、
r = √(x² + y²)
θ= Tan^-1(y/x)
 
直交座標系の円
x = rcosθ
y = rsinθ
より
x²+y² = r²(cos²θ+sin²θ)
x²+y² = r² … 原点からの距離がrの点の集合
 
直交座標系の楕円
長半径a,短半径bの楕円は
半径aの円をy軸方向にb/a倍に伸ばした
形y = (b/a)asinθ = bsinθとなるので
x = acosθ
y = bsinθ
となり
x/a = cosθ
y/b = sinθ
(x/a)²+(y/b)² = cos²θ+sin²θ
x²/a² + y²/b² = 1
となる
この楕円の式を
(Re x, Re y, Im y)座標で描画する
 
楕円の式
x²/a² + y²/b² = 1
より
x² = a² - (a²/b²)y² 
x² = (b²/b²)a² - (a²/b²)y² 
x = ±(a/b)√(b² - y²)
 
y = R+Iiと置くと
x = ±(a/b)√(b² - y²)
= ±(a/b)√{b² - (R + Ii)²}
= ±(a/b)√{b² - (R² - I² + 2RIi)}
= ±(a/b)√{b² - R² + I² - 2RIi}
 
√(X+Yi)を計算する
r = √(X²+Y²), θ=Tan^-1(Y/X)
X+Yi = r(cosθ + isinθ)
√(X+Yi) = r^1/2(cosθ + isinθ)^1/2 
= r^1/2(cos(θ/2) + isin(θ/2))
詳しくは
https://ulprojectmail.blogspot.com/2021/10/n88-basicn-3.html
N88-BASICでn乗の解 (3回目)
を参照して下さい
 
X = b² - R² + I² , Y = -2RI
r = √(X² + Y²), d = (a/b)√r
t = Tan^-1(Y/X)
x = ±(a/b)√{X + Yi}
= ±d(cos(t/2) + isin(t/2))
Re x = ±dcos(t/2), Im x = ±idsin(t/2)
となる
このまま、描画しても良いのですが
三角関数を使わない形に変形すると
 
Z = √{X + Yi}
= √√(X² + Y²)(cos(t/2) + isin(t/2))
Re Z = √√(X² + Y²)cos(t/2)
Im Z = √√(X² + Y²)sin(t/2)
Re x = ±(a/b)Re Z
Im x = ±(a/b)Im Z
 
tanθ = sinθ/cosθ
tan²θ = (1-cos²θ)/cos²θ = 1/cos²θ-1
cos²θ = 1/(1+tan²θ)
 
1-cos²θ = 1-1/(1+tan²θ)
= tan²θ/(1+tan²θ)
1/(1+cosθ) = 1/{1 + 1/√(1+tan²θ)}
= √(1+tan²θ)/{1+√(1+tan²θ)}
 
sin²(θ/2) = (1 - cosθ)/2
cos²(θ/2) = (1 + cosθ)/2
tan²(θ/2) = (1 - cosθ)/(1 + cosθ)
= (1 - cos²θ)/(1 + cosθ)² 
= {tan²θ/(1+tan²θ)}[√(1+tan²θ)/{1+√(1+tan²θ)}]² 
= tan²θ/{1+√(1+tan²θ)}² 
tan(θ/2) = tanθ/{1+√(1+tan²θ)}
x = tanθ, θ = Tan^-1(x)
tan(θ/2) = x/{1+√(1+x²)}
Tan^-1{tan(θ/2)} = Tan^-1[x/{1+√(1+x²)}]
θ/2 = Tan^-1[x/{1+√(1+x²)}]
θ = 2Tan^-1[x/{1+√(1+x²)}]
Tan^-1(x) = 2Tan^-1[x/{1+√(1+x²)}]
 
y = tan{Tan^-1(x)/2}
Tan^-1(y) = Tan^-1(x)/2
Tan^-1(x) = 2Tan^-1(y)
y = x/{1+√(1+x²)}
= x{1-√(1+x²)}/{1-(1+x²)}
= x{√(1+x²)-1}/x² 
= {√(1+x²)-1}/x
1+tan²(Tan^-1(x)/2)
= [x²+{√(1+x²)-1}²]/x² 
= {x²+(1+x²)+1-2√(1+x²)}/x² 
= 2{x²+1-√(1+x²)}/x² 
1/[1+tan²{Tan^-1(x)/2}]
= x²/[2{x²+1-√(1+x²)}]
= x²{x²+1+√(1+x²)}/[2{(x²+1)²-(1+x²)}]
= x²{x²+1+√(1+x²)}/{2(x⁴+1+2x²-1-x²)}
= x²{x²+1+√(1+x²)}/{2(x⁴+x²)}
= {x²+1+√(x²+1)}/{2(x²+1)}
= [1+√{1/(x²+1)}]/2
 
√{X + Yi}
= √√(X² + Y²)(cos(t/2) + isin(t/2))
 
cos²(t/2) = 1/(1+tan²(t/2))
= 1/(1+tan²(Tan^-1(Y/X)/2))
= [1+√{1/((Y/X)²+1)}]/2
= [1+√[1/{(Y²+X²)/X²}]]/2
= [1+√{X²/(Y²+X²)}]/2
= [1+X/√(Y²+X²)}]/2
= {X+√(Y²+X²)}/{2√(Y²+X²)}
= {(Y²+X²)+X√(Y²+X²)}/{2(Y²+X²)}
 
sin²θ = tan²θcos²θ = tan²θ/(1+tan²θ)
= tan²(Tan^-1(Y/X)/2)/(1+tan²(Tan^-1(Y/X)/2))
 
√(X²+Y²)cos²(t/2)
= √(X²+Y²){(Y²+X²)+X√(Y²+X²)}/{2(Y²+X²)}
= {X(Y²+X²)+(Y²+X²)√(Y²+X²)}/{2(Y²+X²)}
= {X+√(Y²+X²)}/2
√(X²+Y²)sin²(t/2)
=√(X²+Y²){1-cos²(t/2)}
=√(X²+Y²)-√(X²+Y²)cos²(t/2)
= √(X²+Y²)-{X+√(Y²+X²)}/2
= [2√(X²+Y²)-X-√(Y²+X²)}]/2
= {-X+√(Y²+X²)}/2
 
Z = √(X±|Y|i)
= √[{X+√(X²+Y²)}/2]±√[{-X+√(X²+Y²)}/2]i
 
まとめ
x²/a² + y²/b² = 1よりx = ±(a/b)√(b² - y²)
y = R+Ii, X = b² - R² + I² , Y = -2RI
Re x = ±(a/b)Re Z = ±(a/b)√[{X+√(X²+Y²)}/2]
Im x = ±(a/b)Im Z = ±s(a/b)√[{-X+√(X²+Y²)}/2]
s = -1 (if Y < 0), s = 1 (if Y > 0)
 
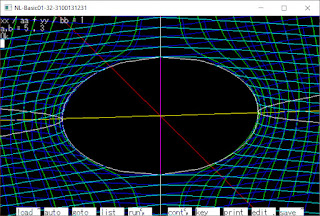
グラフを表示した結果
(Re x, Re y)座標に楕円　(白い線)
(Re x, Im y)座標に双曲線(白い線)
が現れています
これは
x²/a² + y²/b² = 1がyが実数なら楕円
純虚数なら双曲線を表すことを示しています
(Im yを軸に左右の双曲線になる)
 
つまりx,yを実数とすると
x²/a² + y²/b² = 1は楕円
x²/a² - y²/b² = 1はy軸に対して左右の双曲線
-x²/a² + y²/b² = 1はx軸に対して上下の双曲線
になります
放物線はどこかに行ってしまった様です
 
x²/a² + y²/b² = 1のグラフを
(Re x黄, Re y紫, Im y赤)座標に
描画しています
 
NL-BASICとblg～.zip(elli001.bas)は
このブログ(以下のリンク)から
ダウンロードできます

https://ulprojectmail.blogspot.com
Readme.txtを読んで遊んで下さい