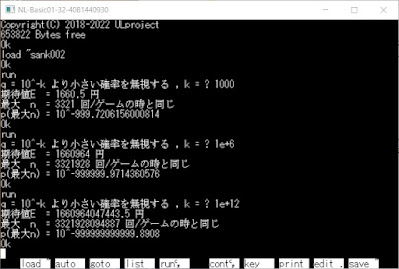
d88ファイルの変換 (2回目)
2022/8/28(日) d88ファイルの変換 (2回目) d88ファイルの紹介と動かし方 N.Matsukawa 様のページ http://www.cad-red.com/basic_magazine/ ディスクイメージのダウンロードで bm88_2ds.lzhをダウンロードする ahirudanna 様のページ http://ahirudanna.html.xdomain.jp/haifu_pc-88.html PC-8801用プログラム集(2012年09月09日更新)から pc-88_02.lzhをダウンロードする https://ulprojectmail.blogspot.com/2022/08/d88-1.html d88ファイル変換 (1回目) の手順でアスキーファイルに変換 出来たファイル ~ .bas を XL-BASICでLOADしてRUNする SCREEN 0を実行しておく必要がある場合があります 動作が速すぎる場合は Alt+4 , Alt+7 , Alt+8 のどれかで遅くなります 動作が遅すぎる場合は Alt+5 , Alt+6 , Alt+9 , Alt+0 , Alt+- , Alt+^ などで速くなります Alt+F2で初期状態になります Beepの音量は初期状態では0で Alt+eで大きく、Alt+rで小さくなります Alt+Eで最大、Alt+Rで0になります テンキーがない PCで テンキーを使用するときは 外付けのテンキーが必要です 動作しないプログラムや 実機と異なる動作をする場合が有ります VL,NL,XL-BASICは 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい