N88-BASICで天体の軌道 (1回目)
2021/10/18(月)
N88-BASICで天体の軌道 (1回目)
離心率 e = c / a = c / (q + c) ≧ 0
近点距離q = a(1 - e) = a - c
遠点距離Q = a(1 + e) = a + c
焦点距離c = ae
長半径 a = q / (1 - e) = q + c
短半径 b = √(a2 - c2) = a√(1 - e2)
半直弦 ℓ = a(1 - e2) = q(1 + e)
動径 r = ℓ / (1 + e cosf)
真近点角f
離心近点角u
(楕)円軌道(e<1)
双曲線軌道(e>1)
放物線軌道(e=1)の順に以下に示します
uをfに変換
tan(f/2) = √{(1+e)/(1-e)}tan(u/2)
tan(f/2) = √{(e+1)/(e-1)}tanh(u/2)
tan(f/2) = u/√(2q)
ケプラー方程式
M = u - esinu
M = esinh(u) - u
M = u3/6 + qu
これらの式の詳しい説明は
https://ulprojectmail.blogspot.com/2021/10/kepler-5.html
天体の軌道(Kepler) (5回目)
https://ulprojectmail.blogspot.com/2021/10/kepler-6.html
天体の軌道(Kepler) (6回目)
https://ulprojectmail.blogspot.com/2021/10/kepler-7.html
天体の軌道(Kepler) (7回目)
を参照して下さい
Mからuを求めるには数値計算するしかなく
ここではニュートン法で解くことにします
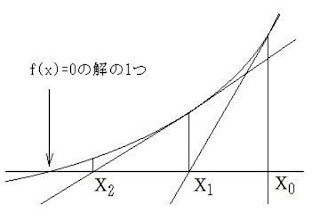
図1. ニュートン法
y = f(x)のxでの接線の傾きは、
微分したy'= f'(x)で、
x = aの時の接線は、
y - f(a) = f'(a)(x - a)より、
y = f'(a)(x - a) + f(a)
これと、x軸(y = 0)との交点は、
f'(a)(x - a) + f(a) = 0より、
x = {af'(a) - f(a)} / f'(a)
x = a - f(a)/f'(a)
xn = a
xn+1 = a - f(a)/f'(a)
と置くと、
xn+1 = xn - f(xn)/f'(xn)
これを、n=0,1,2, ... と繰返すと、
f(x) = 0の解の1つに近づく、
|f(xn)/f'(xn)| < ε(0.01等精度を表す値)
になるまで繰返す
ケプラー方程式 M = u - esinu
f(u) = u - esinu - M = 0
f'(u) = 1 - ecosu
ここで、初期値u0は何でもよいのですが
解に近いほうが良く、離れていると
別の解に収束するかもしれませんので
注意が必要です
sinhの微分
(d/dx)sinhx = (d/dx){exp(x)-exp(-x)}/2
= [exp(x)-{-exp(-x)}]/2
= {exp(x)+exp(-x)}/2
= coshx
ケプラー方程式 M = esinhu - uより
esinhu - u - M = 0なので
f(u) = esinhu - u - M
f'(u) = ecoshu - 1
u0 = M(任意だが解に近いほうが収束が速い)
としています
ここでは、ケプラー方程式を変形して
u = M + esinu
sinu = sinMと近似して、
u0 = M + esinM
を初期値にしています
ケプラー方程式 M = u3/6 + quより
u3/6 + qu - M = 0なので
f(u) = u3/6 + qu - M
f'(u) = u2/2 + q
u0 = M(任意だが解に近いほうが収束が速い)
としています
以下のθの式よりuの式のほうが収束が
速い様です
θを使用したケプラー方程式は
θ = u/√(2q)よりu = θ√(2q)を
ケプラー方程式 M = u3/6 + qu
に代入、M = θ3q√(2q)/3 + θq√(2q)より
ケプラー方程式 3M/{q√(2q)} = θ3 + 3θ
これを使用すると
f(θ) = θ3 + 3θ - 3M/{q√(2q)}
f'(θ) = 3θ2 + 3
θ0 = 3M/{q√(2q)} (適当に選びました)
3次方程式の解法で解く
解法の詳しくは
https://ulprojectmail.blogspot.com/2021/10/n88-basic3-1.html
N88-BASICで3次方程式 (1回目)
を参照して下さい
x3 + px + q = 0
x = α+β, αω+βω2, αω2+βω
α= 3√[-q/2+√{(q/2)2 + (p/3)3}]
β= 3√[-q/2-√{(q/2)2 + (p/3)3}]
(α,βは実数同士または共役複素数)
f(x) = x3 + cx - d = 0 (c > 0)
を求める式でケプラー方程式を解く
f'(x) = 3x2 + c > 0
よりy = f(x) は単調増加のグラフ
なので、実数解は必ず1つとなる
また
(q/2)2 + (p/3)3 = (-d/2)2 + (c/3)3 > 0
よりα,βは実数のみで計算可能で
x = α+βが唯一の実数解となる
M = u3/6 + quのとき
u3 + 6qu - 6M = 0を解く
x = u, d = 6Mと置くと
x3 + 6qx - d = 0
f = d / 2
h = √(f2 + (6q/3)3)
x = 3√(f+h) + 3√(f-h)
u = x
θ = u/√(2q)と置きu = θ√(2q)を
u3 + 6qu - 6M = 0に代入して
θ3 + 3θ - 3M/{q√(2q)} = 0を解く
x = u, d = 3M/{q√(2q)}と置くと
x3 + 3x - d = 0
f = d / 2
h = √(f2 + 1)
x = 3√(f+h) + 3√(f-h)
θ=x
u = θ√(2q)
今回はこれを使用して求めています
N88-BASICはtanh-1(x)がないので
tanh-1(x) = log{(1+x)/(1-x)}/2
を使用しました
詳しくは
https://ulprojectmail.blogspot.com/2021/09/3.html
三角関数 (3回目)
を参照して下さい
プログラムはMを-π~πの範囲(楕円で一周)
πを30等分した間隔で表示しています
おまけ
ニュートン法より収束の速いハレー法
というのがありますので高速化が必要な
場合は、検索して使ってみては
いかがでしょうか
f(x)=0を解く方法で、
xn+1 = xn - g(xn) … (n = 0, 1, ...)
について、
g(x) = f(x) / f'(x)
とすれば、ニュートン法ですが、
g(x) = f(x) / {f'(x) - f''(x)f(x)/(2f'(x)}
とすれば、ハレー法になります
f'(x)はf(x)の1回微分、
f''(x)はf(x)の2回微分です
ケプラー方程式 M = u - esinuの場合、
f(u) = u - esinu - M = 0を解く、
f'(u) = 1 - ecosu
f''(u) = esinu
です
NL-BASICとblg~.zip(plan001.bas)は
このブログ(以下のリンク)から
ダウンロードできます
離心率 e = c / a = c / (q + c) ≧ 0
近点距離q = a(1 - e) = a - c
遠点距離Q = a(1 + e) = a + c
焦点距離c = ae
長半径 a = q / (1 - e) = q + c
短半径 b = √(a2 - c2) = a√(1 - e2)
半直弦 ℓ = a(1 - e2) = q(1 + e)
動径 r = ℓ / (1 + e cosf)
真近点角f
離心近点角u
(楕)円軌道(e<1)
双曲線軌道(e>1)
放物線軌道(e=1)の順に以下に示します
uをfに変換
tan(f/2) = √{(1+e)/(1-e)}tan(u/2)
tan(f/2) = √{(e+1)/(e-1)}tanh(u/2)
tan(f/2) = u/√(2q)
ケプラー方程式
M = u - esinu
M = esinh(u) - u
M = u3/6 + qu
これらの式の詳しい説明は
https://ulprojectmail.blogspot.com/2021/10/kepler-5.html
天体の軌道(Kepler) (5回目)
https://ulprojectmail.blogspot.com/2021/10/kepler-6.html
天体の軌道(Kepler) (6回目)
https://ulprojectmail.blogspot.com/2021/10/kepler-7.html
天体の軌道(Kepler) (7回目)
を参照して下さい
Mからuを求めるには数値計算するしかなく
ここではニュートン法で解くことにします
図1. ニュートン法
y = f(x)のxでの接線の傾きは、
微分したy'= f'(x)で、
x = aの時の接線は、
y - f(a) = f'(a)(x - a)より、
y = f'(a)(x - a) + f(a)
これと、x軸(y = 0)との交点は、
f'(a)(x - a) + f(a) = 0より、
x = {af'(a) - f(a)} / f'(a)
x = a - f(a)/f'(a)
xn = a
xn+1 = a - f(a)/f'(a)
と置くと、
xn+1 = xn - f(xn)/f'(xn)
これを、n=0,1,2, ... と繰返すと、
f(x) = 0の解の1つに近づく、
|f(xn)/f'(xn)| < ε(0.01等精度を表す値)
になるまで繰返す
ケプラー方程式 M = u - esinu
f(u) = u - esinu - M = 0
f'(u) = 1 - ecosu
ここで、初期値u0は何でもよいのですが
解に近いほうが良く、離れていると
別の解に収束するかもしれませんので
注意が必要です
sinhの微分
(d/dx)sinhx = (d/dx){exp(x)-exp(-x)}/2
= [exp(x)-{-exp(-x)}]/2
= {exp(x)+exp(-x)}/2
= coshx
ケプラー方程式 M = esinhu - uより
esinhu - u - M = 0なので
f(u) = esinhu - u - M
f'(u) = ecoshu - 1
u0 = M(任意だが解に近いほうが収束が速い)
としています
ここでは、ケプラー方程式を変形して
u = M + esinu
sinu = sinMと近似して、
u0 = M + esinM
を初期値にしています
ケプラー方程式 M = u3/6 + quより
u3/6 + qu - M = 0なので
f(u) = u3/6 + qu - M
f'(u) = u2/2 + q
u0 = M(任意だが解に近いほうが収束が速い)
としています
以下のθの式よりuの式のほうが収束が
速い様です
θを使用したケプラー方程式は
θ = u/√(2q)よりu = θ√(2q)を
ケプラー方程式 M = u3/6 + qu
に代入、M = θ3q√(2q)/3 + θq√(2q)より
ケプラー方程式 3M/{q√(2q)} = θ3 + 3θ
これを使用すると
f(θ) = θ3 + 3θ - 3M/{q√(2q)}
f'(θ) = 3θ2 + 3
θ0 = 3M/{q√(2q)} (適当に選びました)
3次方程式の解法で解く
解法の詳しくは
https://ulprojectmail.blogspot.com/2021/10/n88-basic3-1.html
N88-BASICで3次方程式 (1回目)
を参照して下さい
x3 + px + q = 0
x = α+β, αω+βω2, αω2+βω
α= 3√[-q/2+√{(q/2)2 + (p/3)3}]
β= 3√[-q/2-√{(q/2)2 + (p/3)3}]
(α,βは実数同士または共役複素数)
f(x) = x3 + cx - d = 0 (c > 0)
を求める式でケプラー方程式を解く
f'(x) = 3x2 + c > 0
よりy = f(x) は単調増加のグラフ
なので、実数解は必ず1つとなる
また
(q/2)2 + (p/3)3 = (-d/2)2 + (c/3)3 > 0
よりα,βは実数のみで計算可能で
x = α+βが唯一の実数解となる
M = u3/6 + quのとき
u3 + 6qu - 6M = 0を解く
x = u, d = 6Mと置くと
x3 + 6qx - d = 0
f = d / 2
h = √(f2 + (6q/3)3)
x = 3√(f+h) + 3√(f-h)
u = x
θ = u/√(2q)と置きu = θ√(2q)を
u3 + 6qu - 6M = 0に代入して
θ3 + 3θ - 3M/{q√(2q)} = 0を解く
x = u, d = 3M/{q√(2q)}と置くと
x3 + 3x - d = 0
f = d / 2
h = √(f2 + 1)
x = 3√(f+h) + 3√(f-h)
θ=x
u = θ√(2q)
今回はこれを使用して求めています
N88-BASICはtanh-1(x)がないので
tanh-1(x) = log{(1+x)/(1-x)}/2
を使用しました
詳しくは
https://ulprojectmail.blogspot.com/2021/09/3.html
三角関数 (3回目)
を参照して下さい
プログラムはMを-π~πの範囲(楕円で一周)
πを30等分した間隔で表示しています
おまけ
ニュートン法より収束の速いハレー法
というのがありますので高速化が必要な
場合は、検索して使ってみては
いかがでしょうか
xn+1 = xn - g(xn) … (n = 0, 1, ...)
について、
g(x) = f(x) / f'(x)
とすれば、ニュートン法ですが、
g(x) = f(x) / {f'(x) - f''(x)f(x)/(2f'(x)}
とすれば、ハレー法になります
f'(x)はf(x)の1回微分、
f''(x)はf(x)の2回微分です
ケプラー方程式 M = u - esinuの場合、
f(u) = u - esinu - M = 0を解く、
f'(u) = 1 - ecosu
f''(u) = esinu
です
NL-BASICとblg~.zip(plan001.bas)は
このブログ(以下のリンク)から
ダウンロードできます