N88-BASICでベクトル (2回目)

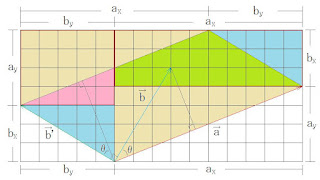
2022/3/6(日) N88-BASICでベクトル (2回目) ベクトルの外積 a,bベクトルの外積cベクトルは、 c = a×b = -b×aで、a,bベクトルが 作る平行四辺形の面積と同じ大きさ で垂直なベクトルになります 向きは、 aからbへ右手の4本指を 向けた時、残りの親指の方向です (aからbへ右ねじを回して進む向き) b x : d = b y : a y より、 b y d = a y b x 図 2 a,bベクトルが作る平行四辺形の面積 a x b y - a y b x a,bベクトルが作る平行四辺形(青+黄)の 面積は、図 2のようになります 黄に注目すると、平行四辺形の面積を変え ずに底辺を水平にすることができます 底辺を水平にした平行四辺形の面積は a x b y - b y d です 紫の三角形は相似なので b x : d = b y : a y より、 b y d = a y b x となり、 紫 +灰?+水色の平行四辺形と 紫 +灰?+桃色の平行四辺形が同じ面積 になり、 a x b y - b y d = a x b y - a y b x です よって、 a,bベクトルが作る平行四辺形 (青+黄)の面積は、a x b y - a y b x となります a,bベクトルが作る平行四辺形の 面積と同じ大きさで垂直なベクトルを cベクトルとすると、 c = (0, 0, a x b y - a y b x ) となります a,bベクトルはxy平面上なので cベクトルはz軸方向になります ここから、 3次元ベクトルを大文字で 表すことにします A = (a x , a y , a z ) B = (b x , b y , b z )として、 A,Bベクトルが作る平行四辺形を x,y,z軸側から見ると x軸 c x ...