ULprojectのホームページ © ULproject

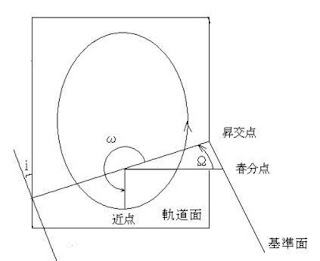
2021/10/17(日) 天体の軌道 (Kepler) (8回目)   図 1. 軌道要素   春分点の方向 γは、 春分の日に地球から見た太陽の方向ですので、 太陽を中心とした春分点方向 に地球が来るのは、秋分の日になります   春分の日は地球の中心位置から見た太陽が 赤道面を南から北へ通過する時間を 含む日です   春分の日と秋分の日は、地球の自転軸の傾き 方向と地球から見た太陽の方向が垂直になる ので、地球の自転軸の傾きが太陽方向には 0 になるため昼と夜の長さが同じになります   昇交点黄経 Ω は、 基準面の惑星 の運動方向にはかった 春分点 から 軌道傾斜軸 (正方向) までの角 です。 (地球の北を上、南を下とすると、惑星が 基準面を下から上に通過する点が、太陽 から見てどの方向かを決定する値です   軌道傾斜角 i は、 昇交点黄経を正軸として基準面に対する軌道面の 傾きを表します。 (傾斜方向は右手系で、正軸を親指とし他の指方向) 基準面はある期間の平均黄道面、不変面などです i= 0～90 ﾟなら 順行 、 90～180 ﾟなら逆行軌道です   近日点引数 ω は、 軌道面の惑星 の運動方向にはかった昇交点から 近 日 点 ( 太陽に一番近づく点 ) までの角 です   近日点黄経 ( Ω+ω ) 、 軌道傾斜角 i =0ﾟで 昇交点 が定義できない時などに、 ω の代わりとして使用する   周期 Pは軌道を 1周するのに必要な時間です   元期平均近点離角 M0 元期 (軌道要素を決定した日)の惑星の位置を 平均近点角 Mで表したものです

2021/10/16(土) 天体の軌道 (Kepler) (7回目)   放物線軌道の tan(f/2) = u/√(2q) M = u 3 /6 + qu ケプラー方程式の導出 (真近点角f, 離心近点角 u ,平均近点角M)   放物線軌道 u: 離心近点角 (放物線用で楕円などと異なる) M:平均近点角 f:真近点角 q:近点距離 r:軌道半径 r = 2q/(1+cosf) (e=1の楕円の式)   f = 90°⇒ r = 2q f = 0°の時の位置を原点とすると f = 90°⇒ P(-q, 2q) y 2  = axに代入して4q 2  = -qa (q > 0) 4q = -a ⇒ a = -4q y 2  = -4qx (q>0, x≦0) r = |( x,y )-(-q,0)| = |(x,√(-4qx))-(-q,0)| 　 = √{(x+q) 2 -4qx } = √{x 2 +2qx+q 2 -4qx } 　 = √{x 2 -2qx+q 2 } = √(q - x) 2   　 = q - x > 0 (q>0, x≦0)   媒介変数 θによる表記   cos2α = cos(α+α) = cos 2 α-sin 2 α = cos 2 α-(1 - cos 2 α) = 2cos 2 α - 1 = (1 - sin 2 α)-sin 2 α = 1 - 2sin 2 α sin 2 ( α/2) = (1 - cosα)/2 cos 2 ( α/2) = (1 + cosα)/2 tan 2 ( α/2) = (1 - cosα)/(1 + cosα) 　　　　　 = (1 - cos 2 α)/(1 + cosα) 2   　　　　　 = sin 2 α/(1 + cosα) 2   tan ( α/2) = sinα/(1 + cosα) より r = 2q/(1+cosf) y = rsinf = 2qsinf/(1+cosf) y = 2qtan(f/2) ここで θ= tan(f/2)と置くと y = 2qθ, x = -y 2 /(4q) = -qθ 2   よって x = -qθ 2   y  = 2qθ r = q - x = q + qθ 2     面積速度を求める   楕円軌道の面積

2021/10/15(金) 天体の軌道 (Kepler) (6回目)   双曲線軌道の tan(f/2) = √{(e+1)/(e-1)}tanh(u/2) M = esinh(u) - u ケプラー方程式の導出 (真近点角f, 離心近点角 u ,平均近点角M)   離心率 e 以下の |1 - e|などはそのまま絶対値記号 を外せる順にしてあります   双曲線軌道 (e＞1) 近点距離 q = a|e - 1| = | c - a| 焦点距離 c = a + q = ae (c > a) a = q / |e - 1| = c - q (a < c) b = √|c 2  - a 2 | = a√|e 2  - 1| 半直弦 L =  a|e 2  - 1| = q(1 + e)   楕円軌道 (0≦e＜1) 近点距離 q = a|1 - e| = |a - c| 焦点距離 c = a - q = ae (c < a) 長半径 a = q / |1 - e| = q + c (a > q) 短半径 b = √|a 2  - c 2 | = a√|1 - e 2 | 半直弦 L = a|1 - e 2 | = q(1 + e)   楕円放物線双曲線共通 (r,f)の関係 真近点角 f 半直弦 L = q(1 + e) 軌道半径 r = L  / (1 + e cosf)   ここでは以後 離心近点角 v(楕円用) 離心近点角 u(双曲線用) として区別することにします   楕円と双曲線の対比 楕円 (円)　　　　　　双曲線 x 2 +y 2 =1　　　　　　　x 2 -y 2 =1 (x,y)=(cosv, sinv)　(x,y)=(±coshu,sinhu) cos 2 v+sin 2 v=1　　　　cosh 2 u-sinh 2 u=1 x 2 /a 2 +y 2 /a 2 =1 　　　　　 x 2 /a 2 -y 2 /a 2 =1 (x,y)=(acosv,asinv)　(x,y)=(±acoshu,asinhu) x 2 /a 2 +y 2 /b 2 =1 　　　　　 x 2 /a 2 -y 2 /b 2 =1 (x,y)=(acosv,bsinv)　(x,y)=(±acoshu,bsinhu)   双曲線関数 eネイピア数(自然対