ULprojectのホームページ © ULproject

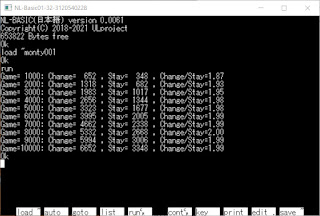
2021/12/8(水) N88-BASICでモンティホール問題 (1回目)   (Monty Hall problem)   A、B、Cの3箱のうち1箱だけ当たりが入っている 1箱選んだ後、残りの2箱の内、外れを1箱開けてもらえる このとき、開いていない残りの箱と交換してもらえるとする   交換する方が得か、交換しない方が得か という問題です   BASICでは、当たりがA-Cのどの箱でも確率は 同じなので、Aが当たりとしてプログラムしました またA-Cは0-2で表しています   走らせると、変えた方が、変えない時より2倍ほど よく当たっています なんだか、不思議です ... が、よく考えてみると、 どれが当たりでも確率はおなじだから、Aが当たりとする   A B C   交換する そのまま   A選ぶ ○ 開 × 1/3 はずれ あたり   × 開 B選ぶ ○ × 開 1/3 あたり はずれ     C選ぶ ○ 開 × 1/3 あたり はずれ         そのままなら、Aを選んでいるときだけ当たりますが、 交換すると、B,Cを選んでいたときに当たります   つまり、変えた方が2倍当たります   交換したときの確率は、2/3 そのままだと、確率は、1/3 です   NL-BASICとblg～.zip(monty001.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい

2021/12/6(月) N88-BASICで2封筒のパラドックス   --------------------------------------------- 封筒のパラドックス --------------------------------------------- 2つの封筒があり、1つの封筒には もう1つの封筒の2倍の金額が入っている AさんとBさんがそれぞれ選んだあと 交換するかを決める   Aの封筒は10000円が入っていた そこでAは考えた 相手は5000か20000のどちらかなので 期待値は(5000+20000)/2=12500となり 10000が12500になると期待できるので 交換した方が得   Bの封筒は20000円が入っていた そこでBは考えた 相手は10000か40000のどちらかなので 期待値は(10000+40000)/2=25000となり 20000が25000になると期待できるので 交換した方が得   交換するとどちらも得になるのはなぜ というパラドックスです   --------------------------------------------- Aさんを考える --------------------------------------------- Aさんが考えたのは交換すると5000か20000が 1/2の確率で得られる場合ですので 前回までの説明通り期待値12500は正しい   しかし、今回はもう一方が20000なので 5000という可能性は0です よってAさんが交換したときの正しい期待値は 5000･0+20000･1=20000です   Aさんは相手の金額を知らないのでこの正しい 期待値を計算できませんが、起こらない5000の 確率を1/2として計算した期待値12500が現実と 一致しないのは当然です   --------------------------------------------- Bさんを考える --------------------------------------------- Bさんが考えたのは交換すると10000か40000が 1/2の確率で得られる場合ですので 前回までの説明通り期待値25000は正しい   しかし、今回はもう一方が10000なので 40000という可能性は0で

2021/12/3(金) N88-BASICでベルトランのパラドックス (2回目) (Bertrand paradox) 円の弦を1本無作為に選び、その長さが、 円に内接する正三角形の辺より長い確率は? を 単位円に長さL＞0の線を投げて弦ができた条件で その弦が円に内接する正三角形の辺√3より長い確率は?   とした考察など 詳しくは https://ulprojectmail.blogspot.com/2021/12/n88-basicbertrand-1.html N88-BASICでベルトランのパラドックス (1回目) を見て下さい   P = [1/2-{π/3+√(3)/2+S 0 }/(2L)]/[1-{(π+S 0 )/(2L)] S 0  = 2[Tan -1 {M/√(1-M 2 )} + M√(1-M 2 )] 0＜L≦√3の時M = 1/ √3＜L＜2の時M = √{1-(L/2) 2 } L≧2の時M = 0 Lを長くしていくとP = 1/2 (L→∞) に収束する L ≦ √3の時はP = 0 (√3より大きい弦は作れない)   L-Pグラフを描画しました   NL-BASICとblg～.zip(bert002.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2021/12/1(水) N88-BASICでベルトランのパラドックス (1回目) (Bertrand paradox)   円の弦を1本無作為に選び、その長さが、 円に内接する正三角形の辺より長い確率は?   弦の選び方で確率が変わるという問題だそうです (確率1/2,1/3,1/4など)   図1 半径r=1の円の場合、正三角形の一辺はa=√3となる aは直角三角形の辺の比 r : a/2 = 2r : a = 2: a = 2 : √3より a = √3 になります   ここで一様分布(偏りのない分布)した弦を考えると その弦の傾き(0°～360°未満)も一様分布しているので 代表で傾き0°の弦のみを考えれば良いことになります 以下、 半径1の円の水平な弦が√3より大きい確率 を考察します   考察1 図2.円周上に一様分布する2点を通る弦   図2の様な場合を考えると 図1より、中心から右半円上の点までの角度が30° の時、弦の長さが√3になるので、0～90°中 0～30°が1/3、30°～90°が2/3の割合なので この場合の確率は1/3になります   しかし、中心近くが疎で一様分布になっていないので この方法で弦を選ぶのは間違いだと思われます   考察2   図1で、円の中心から下半円周に垂直に伸ばした 線分上の一様な点を通る水平な弦を考えると 図2の様な疎密にならないので一様分布と言える   弦の長さが√3(図中のa)になるのは 中心から1/2(図中のr/2)の距離の点を通る時なので 確率は1/2となる   どうやら、1/2が正しそうです (ただし、この場合も問題点があるかもしれません)   考察3 実際に円上にシャーペンの芯などを投げる場合を 考えると芯の長さによって確率が変わるように 思えます そこで、以下の問題を考えて見ます   単位円に長さL＞0の線を投げて弦ができた条件で その弦が円に内接する正三角形の辺√3より長い確率は?   線の中心をP(x,y)とすると 線で弦ができる点Pの範囲は   2√{1-(1/2) 2 } = √3 0＜L≦√3の時M = 1/2 √3＜L＜2の時M = √{1-(L/2) 2 } L≧2の時M = 0 M≦|y|≦1 0≦√(1-y 2 )≦√(1-M 2 ) K = -√(1-y 2 ) + L/2, K≧

2021/11/28(日) N88-BASICでアナログ時計   アナログ時計を表示しました 1,2キーで秒針の動きを変える事が出来ます 1秒毎に動かすのは簡単です   N88-BASICでは1秒以下の時間を計る関数が ありませんので、滑らかに動かすのは大変です   そこで、1秒間で何回針を書き換えられるかを 測定し、1回の書き換えで進むべき時間を求め る事で滑らかに動かしています   余談 AM/PMを使った12時間表示では AM(午前)は00:00～12:00未満 PM(午後)は12:00～24:00未満 なので AM(午前)12:00が00:00(夜) PM(午後)12:00が12:00(昼) ですが   日本の明治?からの法律では 午前は01時0～12時 午後は13時0～24時 となっていて 午後12:00が00:00(夜) 午前12:00が12:00(昼) という事になっています つまり昼の12:30は午前という 大変混乱する法律を 未だに使っているのです 12:00は午前12:00で 12:01は午後12:01という解釈は 更に混乱を呼びます またアナログ時計に存在しない 午後0時などという更に混乱を 招く解釈をする方がいらっしゃいますが   初めに紹介したAM/PMのに解釈すれば すっきりするのだから 解釈を捻じ曲げて現行法を擁護するより 法律の方を変えるほうがすっきりすると 思います   現在ほとんどの方が 昼の12時から午後だという 認識をしていると思いますので (現行法では昼の12時は午前)   早く法改正すべきだと思います   NL-BASICとblg～.zip(clock001.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2021/11/27(土) N88-BASICで素数 (2回目) 素因数分解 数値や式を因数の積の形にする事を 因数分解といいます 素数のみの因数の積で表す事を 素因数分解と言います   数値n(2以上の整数)を素因数分解するには   i = 2～[√n]で割れば良く ([a]はガウス記号でaを超えない最大の整数 a>0なら切り捨て、a<0なら切り上げ)   n = 18なら 2 ) 18 3 )  9 　　 3 18 = 2･3･3 = 2･3 2   となります   アルゴリズム(解法?) ① m = [√n] ② i = 2 ③ i > m なら⑥へ ④ q = n / iが 　 割り切れればiが素因数, n←q ,  m = [√n] 　 割り切れなければi←i+1 ⑤ ③へ ⑥ nが素因数   単純だが遅い方法がその1です   2で割り切れなくなれば あとは偶数では割り切れないので 偶数で割ることを省略して処理速度を 上げたのがその2です   今回はこの2種類のアルゴリズムの 処理時間を比較してみました   探せば処理速度の速いアルゴリズムが いろいろとあると思います   また、C等のコンパイラ言語で書くと もっと速くなります   今回TIME$を使って時間を表示しています NL-BASIC,VL-BASIC,XL-BASICの 時刻(DATE$, TIME$)はCLEARやRUNで、 システム時刻に戻ります   Enterのみ入力した場合 127 * 524287 * 6700417 を計算するようにしています   NL-BASICとblg～.zip(prime002.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2021/11/26(金) N88-BASICで素数 (1回目) 1～10000までの1229個の素数を求める (NL-BASICはAlt+6で高速化)   エラトステネスのふるい(Sieve of Eratosthenes)   1は素数ではないので消します (素因数分解は6=2×3で6=1×2×3ではない) 2は素数なので2より大きい2の倍数を消す (消えていない数は素数と判断) 3は素数なので3より大きい3の倍数を消す 4は2の倍数なので消えている(素数でない) 5は素数なので5より大きい5の倍数を消す … と[√10000]=100まで繰り返し 残った数が素数です ([x]はガウス記号でxを超えない最大の整数)   b>[√n]、n=b×aとするとb≧aとなり nはaの倍数としてすでに消えている つまり[√n]より大きい数の2～n/[√n]倍の数は すでに消えているということです   通常配列を使うところをグラフィック画面に 点を描いて色で判定しています。 (素数でない場合は0:黒)   100×100(1～10000)のマスに残った素数が 描く模様がどのようなものになるのかと思い 描いてみました   NL-BASICとblg～.zip(prime001.bas)は このブログ(以下のリンク)から ダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい