科学,数学,趣味でPC © ULproject

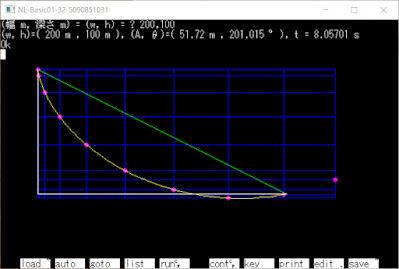
2023/9/18(月) 最速降下曲線 (2回目)   (Brachistochrone curve)   今回は最短経路(直線)の運動を求めて 最速降下曲線と比較する   ■ 問題 重力加速度gのもとで(下向きを正とする) 点A(0, 0)から点B(w, h)に降下するとき 質点P(x, y)の最速降下線を求めよ       ■ 前回 ▼ 軌道 0 ≦ θ ≦ 2π x = A(θ - sinθ) y = A(1  - cosθ) θ = t√(g/A) t = θ√(A/g)   θ = 2π, A = w/2π  (if h = 0)   f(θ) = (θ - sinθ) / (1  - cosθ) - h/w f(θ) = 0の解, A = h/(1  - cosθ)  (if h > 0)     ■ 解法 ▼ 移動距離 傾斜面の長さSは S = √(w 2  + h 2 )   傾斜面の俯角θは tanθ = h/w sinθ = h/S = h/√(w 2  + h 2 ) cosθ = w/S = w/√(w 2  + h 2 )   斜面の移動距離sは s = (1/2)(gsinθ)t 2   = (1/2)gt 2 h/√(w 2  + h 2 ) 移動距離x,yは x = scosθ = sw/√(w 2  + h 2 ) = (1/2)gt 2 wh/(w 2  + h 2 ) y = ssinθ = sh/√(w 2  + h 2 ) = (1/2)gt 2 h 2 /(w 2  + h 2 )   移動率をαとして α = (1/2)gt 2 h/(w 2  + h 2 ) (x, y) = (αw, αh)   時間 t...

2023/9/14(木) N88-BASICで最速降下曲線 (1回目)   (Brachistochrone curve)     ■ 解 https://ulprojectmail.blogspot.com/2023/09/brachistochrone-1.html 最速降下曲線 (1回目) より   ▼ 前提 重力加速度gのもとで(下向きを正とする) 点A(0, 0)から点B(w, h)に降下するとき 質点P(x, y)の最速降下線を求める   ▼ 軌道 0 ≦ θ ≦ 2π x = A(θ - sinθ) y = A(1  - cosθ) θ = t√(g/A)   ▼ h = 0の時のθ,A θ = 2π A = w/2π   ▼ h > 0の時のθ,A (θ - sinθ) / (1  - cosθ) - h/w = 0   ニュートン法 f(x) = 0の解を求める   f(x) = (1 - cosx) / (x - sinx) - h/w f'(x) = (xsinx + 2cosx - 2)/(x-sinx) 2     x  n  ≠ 0, 2π Δx = f(x  n )/f'(x  n ) x n+1  = x  n  – Δx x = x  n  (if Δx < ε)   θ = xを次の式に代入 A = h/(1  - cosθ)     ■ 解説 (w, h)を入力して 1sec毎にgridを描画 軌道を描画     VL,NLと blg～.zip ( brac 00 1 .bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.txtを読んで遊んで下さい  

2023/9/12(火) 最速降下曲線 (1回目)   (Brachistochrone curve)     ■ 問題 重力加速度gのもとで(下向きを正とする) 点A(0, 0)から点B(w, h)に降下するとき 質点P(x, y)の最速降下曲線を求めよ   ベルヌーイ(Bernoulli)が問い ニュートンはpm4:00に仕事が終わり 問題を見てam4:00に解き終わった     ■ 解法 ▼ 総時間t 距離 ds = √(dx 2  + dy 2 ) = dx√(1 + dy 2 /dx 2 ) より ds/dx = √(1 + dy 2 /dx 2 ) dsを進む時間をdtとすると 速度 v = ds/dt = (ds/dx)(dx/dt) … (x方向の速度をs方向に補正) = (dx/dt)√(1 + dy 2 /dx 2 ) よって dt = √(1 + dy 2 /dx 2 ) / v dx = √{(1 + y' 2 ) / v 2 }dx   総時間 t = ∫dt = ∫√{(1 + y' 2 ) / v 2 }dx   高さy=0地点の速度v=0より (1/2)mv 2  + (-mgy) = 0 v = √(2gy)  … ⓪ を代入 t = ∫√{(1 + y' 2 ) / v 2 }dx = ∫√{(1 + y' 2 )/(2gy)} dx   総時間 t = ∫ 0 w  √{(1 + y' 2 )/(2gy)} dx   ▼ 変分法 最速降下曲線からのズレを δy(x)とすると δy(0) = δy(w) = 0 δT(y, y') = T(y+δy, y'+δy') - T(y, y') ≒ (∂T(y,y')/∂y)δy + (∂T(y,y')/∂y')δy'   tの式の積分の中を次の様に置くと t = ∫ 0 w  √{(1 + y' 2 )/(2gy)} dx T(y, y') = √{(1 + y' 2 )/(2gy)}  … ① t = ∫ 0 w  T(y, y') dx なので δt = ∫ 0 w ...

2023/8/10(日) 電磁気学 (5回目)   (Electro magnetics) ローレンツ条件 (Lorenz condition)     ■ 前提 ▼ 定義 ナブラ∇ = (∂/∂x,∂/∂y,∂/∂z) grad f = ∇f , div E  = ∇･ E  , rot E  = ∇× E   ラプラシアン∇･∇ = ∇ 2  = Δ ダランべルシアン □ = ∂ μ ∂ μ  = -(1/c 2 )(∂ 2 /∂t 2 ) + Δ   E     :電場(N/C) B     :磁束密度(T) = (Wb/m 2 ) = (Vs/m 2 ) = (N/(A･m)) ρ   :電荷密度[総量Q:電荷(C)] ε 0 :真空中の誘電率(F/m)[ε:誘電率] μ 0 :真空中の透磁率(N/A 2 )[μ:透磁率] j     :電流密度[総量I:電流(A)] φ   :スカラーポテンシャル(V) A    :ベクトルポテンシャル c   :真空中の光速度(m/s)[c = 1/√(ε 0 μ 0 )導出略]   ▼ 相対論的マクスウェルの方程式 E  = -gradφ - ∂ A /∂t B  = rot A     A μ  = (A 0 , A 1 , A 2 , A 3 ) = (φ/c, A ) j μ  = (j 0 , j 1 , j 2 , j 3 ) = (cρ, j ) □A μ  - ∂ μ (∂ ν A ν ) = -μ 0 j μ     今までの式変形の逆算より {Δ - (1/c 2 )(∂ 2 /∂t 2 )} A   - grad{div A  + (1/c 2 )(∂φ/∂t)} = -μ 0 j   … ① Δφ + div(∂ A /∂t) =  -μ 0 j 0   … ②     ■ 導出 ▼ ゲージ変換 ...

2023/9/6(水) 電磁気学 (4回目)   (Electro magnetics)   (特殊)相対論的マクスウェルの方程式の導出 (Maxwell's equation)   ■ 前提 ▼ 定義 ナブラ∇ = (∂/∂x,∂/∂y,∂/∂z) grad f = ∇f , div E  = ∇･ E  , rot E  = ∇× E   ラプラシアン∇･∇ = ∇ 2  = Δ ダランべルシアン □ = ∂ μ ∂ μ  = -(1/c 2 )(∂ 2 /∂t 2 ) + Δ   E     :電場(N/C) B     :磁束密度(T) = (Wb/m 2 ) = (Vs/m 2 ) = (N/(A･m)) ρ   :電荷密度[総量Q:電荷(C)] ε 0 :真空中の誘電率(F/m)[ε:誘電率] μ 0 :真空中の透磁率(N/A 2 )[μ:透磁率] j     :電流密度[総量I:電流(A)] φ   :スカラーポテンシャル A    :ベクトルポテンシャル c   :真空中の光速度(m/s)[c = 1/√(ε 0 μ 0 )導出略]   ▼ ポテンシャルの方程式 E  = -gradφ - ∂ A /∂t B  = rot A     {Δ - ε 0 μ 0 (∂ 2 /∂t 2 )} A   - grad{div A  + ε 0 μ 0 (∂φ/∂t)} = -μ 0 j   … ① Δφ + div(∂ A /∂t) = -ρ/ε 0   … ②     ■ 導出 ▼ 式の変形 c = 1/√(ε 0 μ 0 )  … 光速度 より ε 0 μ 0  = 1/c 2   を使って {Δ - ε 0 μ 0 (∂ 2 /∂t 2 )} A   - grad{div A  + ε 0 μ 0 (∂φ/∂t)} = -μ 0 j   … ① は {...