N88-BASICで最速降下曲線 (2回目)
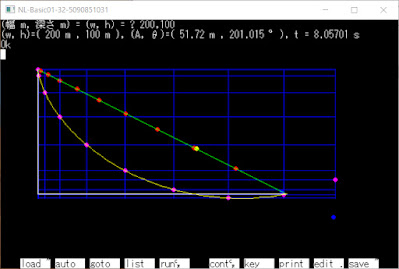
2023/9/20(水) N88-BASICで最速降下曲線 (2回目) (Brachistochrone curve) 最短経路(直線)と比較 ■ 解 https://ulprojectmail.blogspot.com/2023/09/brachistochrone-1.html 最速降下曲線 (1回目) https://ulprojectmail.blogspot.com/2023/09/brachistochrone-2.html 最速降下曲線 (2回目) より ▼ 前提 重力加速度gのもとで(下向きを正とする) 点A(0, 0)から点B(w, h)に降下するとき 質点P(x, y)の最速降下線を求める ▼ 軌道 0 ≦ θ ≦ 2π x = A(θ - sinθ) y = A(1 - cosθ) θ = t√(g/A) t = θ√(A/g) ▼ h = 0の時のθ,A θ = 2π A = w/2π ▼ h > 0の時のθ,A (θ - sinθ) / (1 - cosθ) - h/w = 0 ニュートン法 f(x) = 0の解を求める f(x) = (1 - cosx) / (x - sinx) - h/w f'(x) = (xsinx + 2cosx - 2)/(x-sinx) 2 x n ≠ 0, 2π Δx = f(x n )/f'(x n ) x n+1 = x n – Δx x = x n (if Δx < ε) θ = xを次の式に代入 A = h/(1 - cosθ) ▼ 直線軌道 移動率をαとして α = (1/2)gt 2 h/(w 2 + h 2 ) 移動距離 (x, y) = (αw, αh) 時間 t = √{2α(w 2 + h 2 )/(gh)} ■ 解説 (w, h)を入力して 1sec毎にgridを描画 軌道を描画 直線軌道の時間の点 (紫と赤が対応、それ以外は青) と 最速が終了した時間の点(黄色) を追加 VL,NLと blg~.zip ( brac 00 2 .bas)は 以下のリンクからダウンロードできます https://ulprojectmail.blogspot.com Readme.t